For this assignment you will define a number of utility functions on points and vectors. These functions will be used in multiple parts of the project, so you will define and test them now. You can think of this as defining your own library of functions. You will also define functions for checking the equality of two objects; these functions will simplify your test cases.

Create a hw2 directory in which to develop your solution. You will need to copy your files from the previous assignment to this new directory.

You will develop the new parts of your program solution over two files and you will make changes to data.py from the previous assignment. You must use the specified names for your files.

• vector_math.py - contains the function implementations
• tests.py - contains your test cases

Once you are ready to do so, and you may choose to do so often while incrementally developing your solution, run your program with the command python tests.py.

Download utility.py and place the file in your hw2 directory. You will use the epsilon_equal function defined in utility.py in your solution to this part.

Since you are encouraged to write test cases early, let's begin with some functions that will make writing these test cases less tedious. Modify data.py to add an __eq__ function to each class (i.e., Point.__eq__, Vector.__eq__, Ray.__eq__, and Sphere.__eq__). Each of these functions must be written to compare each of (and all of) the corresponding attributes of the self and other parameters, returning True when all attributes match and False when they do not.

You can review the first part of Lab 3 for additional details.

To summarize, you will implement each of the following equality checking functons.

Point.__eq__(self, other)
Vector.__eq__(self, other)
Ray.__eq__(self, other)
Sphere.__eq__(self, other)

You are to implement the following functions in vector_math.py. These provide basic operations on points and vectors (two of the data types defined in the previous assignment). Details for each function are given in the descriptions that follow. If interested, you will find additional discussion of vectors at http://en.wikipedia.org/wiki/Euclidean_vector.

scale_vector(vector, scalar)
dot_vector(vector1, vector2)
length_vector(vector)
normalize_vector(vector)
difference_point(point1, point2)
difference_vector(vector1, vector2)
translate_point(point, vector)
vector_from_to(from_point, to_point)

Scale

scale_vector(vector, scalar)

This function creates (and returns) a new vector with components equal to the original vector scaled (i.e., multiplied) by the scalar argument.

For example, vector <1, 2, 3> scaled by 1.5 will result in vector <1.5, 3, 4.5>.

Dot Product

dot_vector(vector1, vector2)

This function performs a type of multiplication (product) on vectors. A visualization (via a Java applet) of the dot product can be found here.

The dot product of two vectors is computed as follows.
<x1, y1, z1> * <x2, y2, z2> = x1 * x2 + y1 * y2 + z1 * z2.

As an aside, the dot product is quite useful in calculations between vectors. Specifically, the following is another expression of the dot product.

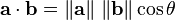
This formula relates the dot product to the angle between two vectors and the magnitude of the vectors. We will use this relationship in the next assignment.

Length

length_vector(vector)

The length of a vector (i.e., its magnitude) is computed from its components using the Pythagorean theorem.

Normalize Vector

normalize_vector(vector)

The function creates (and returns) a new vector by normalizing the input vector. This means that the resulting vector has the same direction but a magnitude of 1. In short, the new vector is the original vector scaled by the inverse of its length.

Point Difference

difference_point(point1, point2)

This function creates (and returns) a new vector obtained by subtracting from point point1 the point point2 (i.e., point1 - point2). This is computed by subtracting the corresponding x-, y-, and z-components. This gives a vector, conceptually, pointing from point2 to point1.

Vector Difference

difference_vector(vector1, vector2)

This functions creates (and returns) a new vector obtained by subtracting from vector vector1 the vector vector2 (i.e., vector1 - vector2). This is computed by subtracting the corresponding x-, y-, and z-components. (Yes, this is very similar to the previous function; the types, however, are conceptually different.)

Translate Point

translate_point(point, vector)

This function creates (and returns) a new point created by translating (i.e., moving) the argument point in the direction of and by the magnitude of the argument vector. You can think of this as the argument vector directing the new point where and how far to go from the argument point.

For example, translating point <9, 0, 1> along vector <1, 2, 3> will result in point <10, 2, 4>.

Vector From To

vector_from_to(from_point, to_point)

This function is simply added to improve readability (and, thereby, to reduce confusion in later assignments). A vector in the direction from one point (from_point) to another (to_point) can be found by subtracting (i.e., point difference) from_point from to_point (i.e., to_point - from_point).

In tests.py, write test cases for each of the above functions (including each of the __eq__ functions). You should place each test case in a separate, appropriately named testing function.

Your test cases must use the unittest module used in lab and discussed in lecture. Create values that are valid arguments to the functions, invoke the functions, and then check that the results are what you expect (as calculated by hand).

You must submit your solution on unix1.csc.calpoly.edu (or on unix2, unix3, or unix4) by 11:59pm on the due date.

The handin command will vary by section.

• Those in Aaron Keen's sections will submit to the akeen user.

  At the prompt, type handin akeen 101hw2 data.py vector_math.py tests.py utility.py

• Those in Julie Workman's sections will submit to the grader-ph user.

  At the prompt, type handin grader-ph 101hw2 data.py vector_math.py tests.py utility.py

• Those in Paul Hatalsky's sections will submit to the grader-ph user.

  At the prompt, type handin grader-ph 101hw2 data.py vector_math.py tests.py utility.py

• Those in John Campbell's sections will submit to the jcampb25 user.

  At the prompt, type handin jcampb25 hw2_XX data.py vector_math.py tests.py utility.py
  where XX is your section number e.g. hw2_13 for 8:10am, hw2_17 for 1:10pm, and hw2_21 for 4:10pm.

Be sure to submit all files that are necessary to run your program (including your files from the previous assignment(s)).

Note that you can resubmit your files as often as you'd like prior to the deadline. Each subsequent submission will replace files of the same name.

The grading breakdown for this assignment is as follows.

• Clean Execution: 10% — Program runs without without crashing (and the submitted source demonstrates a legitimate attempt at a solution).

• Test Cases: 25% — Test cases are provided for each of the implemented functions. The number of test cases is appropriate for the complexity of the corresponding function (with a minimum of two test cases).

• Functionality: 65% — Required functionality has been implemented.