In this assignment you will implement the core intersection mechanic for the ray casting project. More specifically, you will write a number of functions to determine the set of spheres with which a ray intersects.

Create a hw3 directory in which to develop your solution. You will need to copy your files from the previous assignment into this directory.

You will develop the new parts of your program solution over two files. You must use the specified names for your files.

• collisions.py - contains the function implementations
• tests.py - contains your test cases

Once you are ready to do so, and you may choose to do so often while incrementally developing your solution, run your program with the command python tests.py.

To check that your test cases are syntactically correct, you will need to write your test cases and then compile with python -m py_compile tests.py. This will compile your source file (and report syntax errors) without executing the test cases. You should do this before submitting your test cases for the first deadline.

You are to implement the following functions.

sphere_intersection_point(ray, sphere)
find_intersection_points(sphere_list, ray)
sphere_normal_at_point(sphere, point)

In collisions.py implement each of the functions as specified in the following descriptions.

Single Ray-Sphere Intersection

sphere_intersection_point(ray, sphere)

Partial Function?

The purpose of this function is to determine if the given ray intersects the given sphere. If they intersect, then the point at which they intersect is returned (as a Point object). If they do not intersect, then the function should return None. You should note that the function is returning a different type when there is an intersection than when there is not. This is because an intersection function is essentially a partial function (i.e., for some inputs there is no reasonable point of intersection). We will use None to indicate that there is no intersection and leave it to the invoker of this function to check for this case on return.

Functionality

In collisions.py define the sphere_intersection_point function using the algorithm described next.

Ray-Sphere Collision Algorithm

The reasoning behind the functionality.

Is a point on a sphere?

Consider a sphere, theSphere, somewhere in three-dimensional space. This sphere has a location (theSphere.center) and a radius (theSphere.radius). Consider a point on the sphere (and recognize that this holds for every such point). The distance between this point and the center is, of course, equal to the radius.

This fact is great. If we have a point (any point), we can determine if that point is on the sphere by comparing its distance from the sphere's center against the radius. But we do not yet have a point to check.

Recall the following definition of the dot product from the previous assignment.

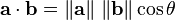
This equation relates the dot product to the angle between two vectors and the magnitude of each vector. If we compute the dot product of a vector with itself, then the angle between them is 0 and, thus, the dot product gives the magnitude squared.

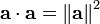
With this in mind, we can use the dot product to determine if a point p is on a sphere theSphere (we will do this because it turns out that using the vector functions simplifies the computation). Which vector do we want? The vector from the center of the sphere to the point. This gives the following.

(p - theSphere.center) ˙ (p - theSphere.center) = theSphere.radius²

Which point should be checked?

With the above it is relatively straightforward to determine if a point lies on a sphere (in fact, you have already implemented the dot product function). But now we need a point to check. It would obviously take far too much time to check for all such points, something we neither want nor need to do. Instead, the only points of interest are those along the ray being cast into the scene.

Recall that a ray (theRay) has both a point of origin (theRay.pt) and a direction (theRay.dir). All points along the ray can be found by transating the ray's origin in the ray's direction. This is a lot of points, but we can parameterize the equation as follows.

point_t = theRay.pt + t * theRay.dir, t ≥ 0

This equation states that a point is found by scaling the direction vector by some parameter t and then translating the ray's origin by the resulting vector. But this equation itself does not give a specific point of interest and there are far too many values to consider for t. Here's where the math comes in.

The math.

Let's take the two previous equations. The second is an equation for all points along a ray. The first is a means to check if a point is on a sphere.

(p - theSphere.center) ˙ (p - theSphere.center) = theSphere.radius²
point_t = theRay.pt + t * theRay.dir, t ≥ 0

Let's combine them.

((theRay.pt + t * theRay.dir) - theSphere.center) ˙ ((theRay.pt + t * theRay.dir) - theSphere.center) = theSphere.radius²

The resulting equation is a lot to look at but essentially asks which point along the ray intersects the sphere. Or, another view, what value of t gives a point along the ray that intersects with the sphere?

This equation can be transformed a bit into the more familiar form of the quadratic equation.

(theRay.dir ˙ theRay.dir) t²
+ (2 * (theRay.pt - theSphere.center) ˙ theRay.dir) t
+ (((theRay.pt - theSphere.center) ˙ (theRay.pt - theSphere.center)) - theSphere.radius²)
= 0

Or.

A t²
+ B t
+ C
= 0

Giving.

A = (theRay.dir ˙ theRay.dir)
B = (2 * (theRay.pt - theSphere.center) ˙ theRay.dir)
C = (((theRay.pt - theSphere.center) ˙ (theRay.pt - theSphere.center)) - theSphere.radius²)

The value of t can now be computed by solving the quadratic equation. As you may recall, this may give 0, 1, or 2 real roots. If there are 0 real roots (i.e., the discriminant is negative), then the ray does not intersect the sphere. If there is one real root, then the ray glances the surface of the sphere colliding at a single point. If there are two real roots, then the ray intersects the sphere at two points passing into and then out of the sphere; the point nearest the origin of the ray (but as computed only by non-negative t values) is the closest intersection point.

To do.

Wow, that was a lot of setup, but with the quadratic equation solved you can determine the nearest intersection point.

Implement the sphere_intersection_point function. If the ray intersects the sphere, then return a Point object with the coordinates of the nearest (to the ray's origin point) intersection point. If the ray does not intersect the sphere, then return a None indicating that the point is not valid.

Consider some of the possible (real) t values.

• Both t values are non-negative (i.e., zero or positive). This implies that the sphere is "in front" of the ray (or, in the zero case, that the ray starts on the sphere) and the ray passes into and then out of the sphere. The smallest of these values gives the desired point of intersection.
• Both t values are negative. This implies that the sphere is "behind" the ray. As such, there is no true intersection with the sphere (so the function should return None).
• One t value is non-negative and the other is negative. This implies that the ray originates inside of (or on) the sphere and intersects on the way out. The non-negative t gives the desired point of intersection.
• If there is only a single root, then the above still applies, it just means the ray intersects on the surface but does not pass through. If t is negative, then the intersection point is not of interest.

But we do not actually want the t value. Wait, what?

The computed t value, if there is a real one, is not what this function will return. Instead, it must return the point of intersection. This point can be found by using the equation given earlier (shown again below).

point_t = theRay.pt + t * theRay.dir, t ≥ 0

Recall that this equation states that the point is found by scaling the direction vector by t and then translating the ray's origin by the resulting vector.

All Ray-Sphere Intersections

find_intersection_points(sphere_list, ray)

After the discussion for the previous function, you may be thinking "oh, dear, here it comes." Fear not, this function uses the work of the previous function to gather all intersections for a given ray.

Functionality

In collisions.py define the find_intersection_points function. This function checks for an intersection between the given ray and each sphere in the sphere_list list. This function will return a list of pairs (i.e., a tuple with two values) representing the found intersections; each pair will contain, in this order, a Sphere and a Point.

For each sphere in the input list, if the ray intersects (determined using the sphere_intersection_point function), add a pair to the list to be returned containing the sphere and the intersection point. The returned list will only contain pairs representing intersections and they should be ordered relative to the input list. As such, the first intersection found will be stored in the 0^th position of result list, the second intersection found will be stored in the 1^th position of the result list, and so on.

This function is really just an elaborate example of the filter pattern.

Sphere Normal

sphere_normal_at_point(sphere, point)

With a point on a sphere found, the normal vector at that point will be of use in the next assignment to determine if the viewer can see the point. The normal vector is a vector (with magnitude 1) along which the center of the sphere must move to reach the point (colloquially referred to as a vector from the center to the point on the surface). Conceptually, this vector is going "from the center out". This can (and should) be computed using functions from the previous assignment.

Functionality

In collisions.py define the sphere_normal_at_point function. Compute the normal vector for the provided sphere at the provided point. (This vector must normalized so that its magnitude is 1.)

In tests.py, write test cases for each of the above functions. You should place each test case in a separate, appropriately named testing function.

Your test cases must use the unittest module used in lab and discussed in lecture. Create values that are valid arguments to the functions, invoke the functions, and then check that the results are what you expect (as calculated by hand).

Hints

• When testing collisions, choose a few "easy" spheres and rays (e.g., those along an axis) and at least one "non-easy" sphere and ray.

• When testing a function that returns a list, it is often helpful to compare the result directly against an "expected" list that you create explicitly in your testing function. This assumes, of course, that the contents can be compared for equality using __eq__ (which is the case for our data values).

You must submit your solution on unix1.csc.calpoly.edu (or on unix2, unix3, or unix4) by 11:59pm on the due date.

The handin command will vary by section.

• Those in Aaron Keen's sections will submit to the akeen user.

  To submit your test cases, at the prompt, type handin akeen 101hw3tests tests.py

  To submit your completed assignment, at the prompt, type handin akeen 101hw3 data.py vector_math.py collisions.py tests.py utility.py

• Those in Julie Workman's sections will submit to the grader-ph user.

  To submit your test cases, at the prompt, type handin grader-ph 101hw3tests tests.py

  To submit your completed assignment, at the prompt, type handin grader-ph 101hw3 data.py vector_math.py collisions.py tests.py utility.py

• Those in Paul Hatalsky's sections will submit to the grader-ph user.

  To submit your test cases, at the prompt, type handin grader-ph 101hw3tests tests.py

  To submit your completed assignment, at the prompt, type handin grader-ph 101hw3 data.py vector_math.py collisions.py tests.py utility.py

• Those in John Campbell's sections will submit to the jcampb25 user.

  To sumbit your test cases, at the prompt, type handin jcampb25 hw3tests_XX tests.py
  where XX is your section number e.g. hw3tests_13 for 8:10am, hw3tests_17 for 1:10pm, and hw3tests_21 for 4:10pm.

  To submit your completed assignment, at the prompt, type handin jcampb25 hw3_XX data.py vector_math.py collisions.py tests.py utility.py
  where XX is your section number e.g. hw3_13 for 8:10am, hw3_17 for 1:10pm, and hw3_21 for 4:10pm.

Be sure to submit all files that are necessary to compile your program (including your files from the previous assignment(s)).

Note that you can resubmit your files as often as you'd like prior to the deadline. Each subsequent submission will replace files of the same name.

The grading breakdown for this assignment is as follows.

• Clean Execution: 10% — Program runs without crashing (and the submitted source demonstrates a legitimate attempt at a solution).

• Test Cases: 25% — Test cases are provided for each of the implemented functions. The number of test cases is appropriate for the complexity of the corresponding function (with a minimum of two test cases).

• Functionality: 65% — Required functionality has been implemented.