CSC 102 Lecture Notes Week 6
GUIs (Graphical User Interfaces) using the Processing IDE
Linked Lists and Abstract Data Types



  1. Relevant reading.

    1. Chapter 14, Sections 1,6,7 -- Introduction to Sorting and Searching

    2. Chapter 15, Sections 1-3 -- Abstract Data Types

    3. Processing Development Environment documentation


  2. Lab 11 and Program 4 Discussions -- see the writeups

    1. Lab 11

    2. Program 4

    3. Our in-class discussion of these will include some running examples using Processing.


  3. Introduction to Data Structures (Ch 15)

    1. Arrays and ArrayLists are key data structures.

    2. There are many more.

    3. The primary purpose of a data structure is support for efficient computation.


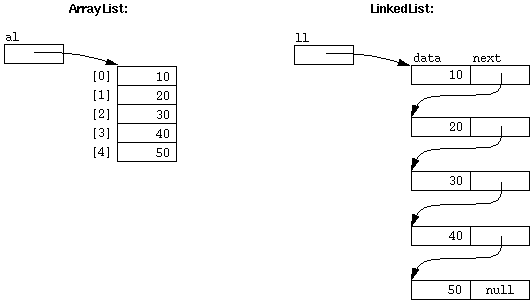
  4. Let's consider a new LinkedList data structure (Sections 15.1, 15.2).

    1. ArrayList elements are in a sequential block.

    2. LinkedList elements are in separate nodes, with links referring to neighboring elements.

    3. Here's some code, from 102/examples/ArrayListAndLinkedListExample.java 
      import java.util.*;
/****
 *
 * This is a very simple example of a 5-element list of integers, declared as
 * both an ArrayList and a LinkedList.  The interesting thing is the picture of
 * how memory looks inside the data abstractions:
 *                                                                          <p>
 *     <img src = "ArrayAndLinkedListPictures.jpg">
 *                                                                          <p>
 * This example uses a couple handy utility methods that convert between lists
 * and arrays -- <tt>asList</tt> and <tt>toArray</tt>.  These are defined in
 * the class java.util.Arrays.  Check out its javadoc <a href=
 * http://java.sun.com/javase/6/docs/api/java/util/Arrays.html> here </a>.
 *
 */
public class ArrayListAndLinkedListExample {
    public static void main(String[] args) {

        /* Declare and initialize the ArrayList. */
        ArrayList<Integer> al =
            new ArrayList<Integer>(Arrays.asList(10,20,30,40.50));

        /* Declare and initialize the LinkedList. */
        LinkedList<Integer> ll =
            new LinkedList<Integer>(Arrays.asList(10,20,30,40.50));

        /* Show that the lists are equal as arrays. */
        System.out.println(Arrays.equals(al.toArray(), ll.toArray()));
    }
}

    4. Here's a picture of what the internal data structures look like in this example:



  5. Abstract Data Types ADTs (Sec 15.3)

    1. "Abstract" means that "details are left out."

    2. What's left out of an ADT is public access to class data structures, e.g., what's shown in the picture above.

    3. E.g., the user of a LinkedList or ArrayList cannot directly access the internal data.

    4. Public methods provide efficient access, based on data structures used (but hidden) in the class.


  6. Measuring data structure efficiency.

    1. Even though the internal data structures are hidden from outside access, understanding the structures is important to understanding the operational efficiency of an ADT.

    2. The efficiency of ADT operations is expressed in terms of operation execution time, based on the number of structure elements, n.

      1. Broadly, efficiency is measured as an order of magnitude of n.

      2. The notational shorthand is "O(f(n))", for some function f; this is called "big-Oh" notation.

    3. Here are some common names used to refer to different levels of efficient, from most to least efficient:
      • O(1) -- constant time
      • O(n) -- linear time
      • O(log(n)) -- log time
      • O(n2) -- quadratic time

    4. Here are comparative efficiencies for key operations in an ArrayList versus LinkedList (see Table 3, Page 649 of the book):

      Operation ArrayList LinkedList Discussion
      random access O(1) O(n) Random access into an array is O(1) because an array is structured like underlying computer memory for which random access is inherently efficient. In contrast, random access to a linked list is O(n) because you always need to find the nth element by starting at the beginning of the list and counting up to the nth element, which on average takes O(n) time.
      find next O(1) O(1) Finding the next element is O(1) for both types of list. For an array, it's just random access to the i+1 when you're at the ith element. For the linked list, next is a matter of following just one next reference
      add/remove O(n) O(1) Adding and removing are O(n) for an array because the both involve moving blocks of elements to make room for an added element or removing an existing element, which on average takes O(n) time. For a linked list, adding and removing are O(1) since they only involve changing a fixed number of node references.

    5. Understanding these efficiencies involves understanding the data structures of the ArrayList and LinkedList ADTs, as pictured above, and discussed in Chapter 15 of the book.

    6. We'll go over some examples during lecture in class, and further in the Week 7 Notes.


  7. Sorting, Chapter 14, Section 1

    1. The basic idea:

      1. search through a list, comparing items

      2. put the smaller ones earlier in the list, the larger ones later

      3. when everything is in its correct place, you're done

    2. Formally, "everything is in its correct place" is defined as:

      forall i, suchthat i >= 0 and i < list.size - 1
      list[i] < list[i+1]


  8. Selection Sort (Section 14.1)

    1. The first section of Chapter 14 in the book is an very good example of sorting.

    2. It shows the actions of one of the simpler forms of sort called selection sort.

    3. We'll go over this example in class.

    4. The book's code example is in 102/examples/book/ch14/selsort

    5. You'll also implement a version of selection sort in lab 12.


  9. Searching, Chapter 14, Sections 6 and 7.

    1. You've already done some basic forms of search in CSC 101, where you use a loop to look for an element in an array, e.g., 
      /****
 * A quick example of search for the element of an array.
 */
public class BasicLinearArraySearch {

    /**
     * Search an int array for a particular number.  Return the first index
     * of the number if it's found, -1 if not found.
     */
    public static int searchArray(int a[], int n) {
        for (int i=0; i<a.length; i++) {
            if (a[i] == n) return i;
        }
        return -1;
    }

    /**
     * Search for a number that's found and another that's not found.
     */
    public static void main(String[] args) {
        int a[] = {10, 20, 30, 40, 50};
        System.out.println("searchArray(a, 40) = " + searchArray(a, 40));
        System.out.println("searchArray(a, 45) = " + searchArray(a, 45));
    }

}

      1. This form of search takes O(n) time since on average you need to look through half of the elements.

      2. In the worst case, when the element you're searching for is at the end of the array, you need to search through all of the elements.

    2. A more efficient form of search is possible when the elements of a list are sorted -- it's called binary search


  10. Binary Search (Section 14.7)

    1. The basic idea:

      1. start the search in the middle of a sorted list

      2. if the item you're looking for is less than the item at the middle, continue the search in the first half of the list, otherwise in the second half

      3. continue this process until you've looked through all the possible elements, which will be at most log2 of them (think about this).

    2. Section 14.7 of the book has a good example of this and we'll go over it in class during lecture.

    3. The book's code example is in 102/examples/book/ch14/binsearch