CSC 103 Lecture Notes Week 5, Part 2
More on Hashing



  1. The lower-level data structure view of a hash table.
    1. Figure 1 in part 1 of this week's notes showed the "textbook" view of a hash table.
    2. Figure 1 below shows the lower-level data structure view of the hash table.

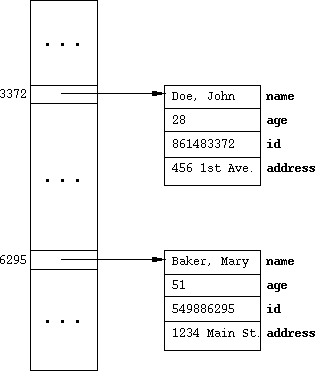
      Figure 1: Low-level data structure view of a hash table.



      1. The concrete representation of the table is the hash table array.
      2. The array contains references to instances of hash table entry objects.
      3. In this case, the entries are four-field information records.

  2. Overview of collision resolution strategies.
    1. As discussed last time, a key issue in hash table design is determining the best way to resolve collisions when the hashing function returns the same table index for two different keys.
    2. There are two major categories of collision resolution.
      1. Out-of-table chaining (called separate chaining in the book).
      2. In-table placement (called open addressing in the book).

  3. Out-of-table chaining for collision resolution.
    1. The approach for out-of-table chaining is to place colliding entries in a linked list, pointed to by the elements of the hash table array.
    2. This is the approach most widely used in practice, such as in libraries like the Java Foundation Classes (JFC).
    3. It is also the approach you will used in Assignment 3.
    4. Section 5.3 in the book has some sample code; your code for Assignment 3 will differ accordingly, to meet the assignment specifications.
    5. The following are basic techniques for implementing hashing methods using out- of-table chaining:
      1. insert(entry)
        1. compute the hash index for the key of the given entry
        2. if the indexed location is empty, add the entry as the first element of a linked list pointed to by table[index]
        3. if the indexed location already has an entry or entries, search the list pointed to by table[index] for an entry with the same key as the entry be inserted
        4. if such an entry is found, return without doing anything, thereby ignoring duplicate entries
        5. if there is no same-key entry, splice the new entry onto the front of the linked list pointed to by table[index]
      2. lookup(key)
        1. compute the hash index for the given key
        2. if the indexed location is empty, fail by returning null
        3. if the indexed location points to a list, search the list for an entry with the same key as that passed to lookup
        4. if such an entry is found in the list, return it, otherwise fail
      3. delete(key)
        1. compute the hash index for the given key
        2. if the indexed location is empty, return without doing anything
        3. if the indexed location points to a list, search the list for an entry with the same key as that passed to delete
        4. if such an entry is found, remove it from the list, otherwise do nothing

  4. In-table collision resolution.
    1. The approach for in-table resolution is to find an empty location in the table by "probing" through the table.
      1. On insert, each probe moves some distance away from the location of the collision, searching for an empty location to insert the new entry.
      2. For lookup and delete, we follow the same probing pattern used for insert, searching for an entry of the desired key.
    2. Linear probing
      1. Linear probing is the simplest form of in-table collision resolution.
      2. The name comes from the fact that a the linear function is used for the probing pattern.
      3. Namely, probe(index) = (index + 1) mod tableSize
      4. That is, the probing search goes sequentially from the collision index, to successive indices below it, wrapping around to the top of the table if necessary.
      5. The probing stops when the search fully wraps around to the original index, meaning that the table is completely full.
      6. The HashTable below has the complete implementation details for linear probing.

    3. Quadratic probing
      1. A potentially significant disadvantage of linear probing is that of secondary collisions due to clustering.
        1. A secondary collision occurs when a key K hashes to location L, but L is already occupied by an entry that was put there because of a previous collision.
        2. This means that collisions can occur for two reasons:
          1. Primary collisions are the result of the hash function returning the same index for two different keys.
          2. Secondary collisions are the result of a hash function returning the index of a location that is filled because of an earlier collision.
        3. Clustering is the effect caused by linear probing of having a number of collisions "bunch up" around a single location.
        4. As the clustering increases, the time it takes to perform the linear probing search will increase.
      2. One solution to avoid secondary collisions is out-of-table chaining.
      3. An in-table approach to avoid clustering is to change the probing function from linear to something else, the most typical case being a quadratic function of the form probe(index) = (index + i2) mod tableSize, for i = 1, ....
        1. Care must be taken when using quadratic probing to ensure that the probing pattern provides adequate coverage of the table.
        2. A useful strategy is to make the size of the table a prime number.
        3. As discussed in Section 5.4.2, of the book, this will ensure adequate coverage with the table is up to half full.
        4. Other strategies are to pick other non-linear probing functions, such as a quadratic residue, that will guarantee full table coverage.
    4. Double hashing
      1. A final approach to in-table collision resolution is to use a second hashing function to provide the search pattern.
      2. That is, we define a probing function of the form probe(index) = index + hash2 + 2 * hash2(index) + ....
      3. This approach requires careful selection of the secondary hash function, again to ensure full coverage of the table by the probing pattern.
    5. In the end, out-of-table chaining has be widely accepted in practice, due to its relative simplicity of implementation and the fact that it avoids many of the problems found with in-table resolution.

  5. The load factor of a hash table.
    1. A hash table's load factor is defined as the ratio of the number of entries to the table size.
    2. An important consideration in hashing performance is value of the load factor.
    3. As the load factor increases, the performance will degrade because of the time required to search collision chains.
    4. We will discuss some analytic results of hash table performance in next week's notes.

  6. Rehashing when a table becomes overly crowded or completely full.
    1. When a table becomes completely full (with in-table resolution), or effectively (with out-of-table resolution), it is necessary or desirable to reallocate the hash table array.
    2. This entails:
      1. allocating a new array, of say twice the size of the original
      2. re-entering all of the existing keys by rehashing them all

  7. The design and implementation of a HashTable class with linear probing collision resolution.
    1. Attached to the notes are the code listings for a HashTable class, plus auxiliary classes for hash table entries, exception handling and testing.
    2. We will discuss the details of these classes in lecture and further in lab.



index | lectures | labs | handouts | examples | assignments | solutions | doc | grades | help