Test Case Result (size '()) 0 (size 'x) 0 (size '(x)) 1 (size '( () (((())) x) () (()()))) 1 (size '(a b c)) 3 (size '(((((a)))) (b (b (b c) d) e) (c d) () f)) 10
Note that a good solution for xunion uses the Lisp member function. However, the requirement that the duplicate equality test be equal as opposed to eq means that you'll have to invoke member in the following extended form:
Test Case Result (xunion '() '()) NIL (xunion '(a b c) '(a b c)) (A B C) (xunion '(b c a) '(a b c)) (A B C) (xunion '(a (a b c) b x z) '(a (a b c) x b y)) (Z A (A B C) X B Y)
This call tests if element e is a member of list l using the equal function instead of the default eq. See Section 15.2 of the online Lisp reference manual for further details.(member e l :test 'equal)
Assume the input tree is represented in the form presented in Section 7.3.2 of the Lisp primer. That is, the general format of a Lisp tree representation is
( root subtree1 ... subtreen )where root must be an atom, and each subtree is an atom or list.
The output of traverse is a list of tree nodes in traversal order. Here are (all of) the test cases:
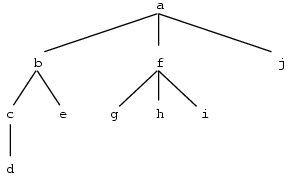
To help visualize the tree structure, here is a traditional picture of the Lisp tree
Test Case Result (traverse '()) NIL (traverse '(a)) (A) (traverse '(a b)) (B A) (traverse '(a b c)) (B C A) (traverse '(a b c d e)) (B C D E A) (traverse '(a (b (c d) e) (f g h i) j)) (D C E B G H I F J A)
(a (b (c d) e) (f g h i) j):