- Go over syllabus
- Pass around 1st-day roster
Standard textbook definition -- a systematic notation to describe a computational process.
-
For the most part, we will be examining what is called the von Neumann
class of programming languages.
-
Briefly, this is the class of languages that have memory variables and
represent computation as a linear sequence of executable statements.
-
Most of the main languages we will study -- Java, C, Perl, Lisp -- fall into
this general category.
-
We will also look at some principles of non-von Neumann languages by
focusing on the functional subset of Lisp, and the declarative languages Yacc
and Lex.
-
There are two interesting subclasses of von Neumann languages that we will
consider, by focusing on features of Java that you probably have not covered in
your earlier classes:
-
concurrent programming languages, as represented by Java threads
- reflective languages, by examining the reflection features of Java, and the programs-as-data features of Lisp.
-
concurrent programming languages, as represented by Java threads
-
HLPLs compared to natural languages:
-
HLPLs are formally less expressive; i.e., PLs are a different formal class than
are natural languages.
-
HLPLs must be unambiguous.
-
HLPLs must be drastically simpler than natural language in order to provide
efficient translation.
- HLPLs are machine-oriented, more than they are human-oriented.
-
HLPLs are formally less expressive; i.e., PLs are a different formal class than
are natural languages.
-
HLPLs compared to mathematical (non-von Neumann) languages:
-
HLPLs have variables that represent physical memory that retains its state
through time; mathematical variables do not have these physical/temporal
properties.
-
E.g., compare
as a Java or C programming language statement versusx = y
as a mathematical statement.x = y
- The latter is a statement of fact whereas the former denotes the process of evaluating y and moving its value into x.
-
E.g., compare
-
A fundamental concept of HLPLs is that of time passing in a sequence of
discrete steps; mathematical languages in general do not have this concept.
-
E.g., compare
as a program versusx = y; x = z;
as a mathematical statement.x = y and x = z
- The latter means that x and y and z are all equal; the former means something quite different than this.
-
E.g., compare
- It is noteworthy that there is much research work devoted to the development of programming languages that behave more like pure mathematics; as noted above, we will look at some of the ideas in such non-von Neumann during the class.
-
HLPLs have variables that represent physical memory that retains its state
through time; mathematical variables do not have these physical/temporal
properties.
-
HLPLs compared to assembly and machine languages:
-
Conceptually, HLPLs and assembly languages are really in the same class --
i.e., both are von Neumann class languages.
- What assembly languages lack is largely a matter of notational convenience.
-
Conceptually, HLPLs and assembly languages are really in the same class --
i.e., both are von Neumann class languages.
-
Sequential HLPLs compared to concurrent HLPLs.
-
Sequential PLs can only express computations with a single thread of control --
executable statements can only run one at a time.
- Concurrent HLPLs have capabilities to express computations in which two or more statements may execute at the same time.
-
Sequential PLs can only express computations with a single thread of control --
executable statements can only run one at a time.
-
Socio-cultural-economic reasons.
- Different application domains are better served by some languages than others.
-
Figure 1 depicts a generational history of HLPLs (cf Figure 1.3 on Page 11 of
the book).
0th Generation: machine and assembly languages
1st Generation: FORTRAN
2nd: academic AI/symbolic systems commercial misc ALGOL 60 SNOBOL LISP COBOL BASIC
2.5th: ALGOL68 Pascal Specialized BCPL, BLISS BASIC+, SIMULA67 LISP FORTH derivatives C
2.75th: Euclid, Clu, Modula Mesa, Alphard, Conc. Pascal
Smalltalk
2.9th: Ada Modula-2 Perl Icon Scheme C++ Ada,C++ PostScript
SR Interlisp, MacLisp, ZetaLisp, etc.
2.95th: Java Dylan Java, C#
3rd: Prolog, ML, LISPs, Prologs, SISAL Lucid, OBJ3 Lex, Yacc
4th: Hypercard REFINE RN SQL AccessFigure 1: Generational history of programming languages.
-
Prominent 2nd, 3rd, and 4th generation developments:
- Modularity and object-oriented features (Simula, Smalltalk, Modula, C++, Java).
- Concurrency (Ada, SR, MultiLisp, ParLOG, Java).
- Functional programming (Lisp, SISAL, ML, OBJ).
- Logic programming (OBJ, Prolog).
- Very-high-level declarative programming (Prolog, OBJ, REFINE).
- GUI, event-based support (Smalltalk, Java).
- Integration of language and its environment (LISPs, SmallTalk, Java).
- Domain-specific languages (Access, SQL).
-
One last note on history --
- Simula 67 is a serious historical omission from the object-oriented languages in the book's Figure 1.3.
- Simula is widely acknowledged to be the first object-oriented language, having introduced the keyword "class" into the PL lexicon, and having inheritance features very much like languages of today, including C++, Java, and C#.
-
Expresses the form (or grammar) of a program in a particular
language.
-
It does not express at all what a program means.
- In other words, syntax expresses what a program looks like but not what it does.
-
An alphabet of symbols that comprise the basic elements of the
grammar.
-
The symbols are comprised of two sets -- terminal symbols (also known
as tokens) and non-terminal symbols (referred to as
grammatical categories in the book).
-
Terminals are those symbols that cannot be broken down into constituents.
- Non-terminals are those symbols that can be broken down further.
-
Terminals are those symbols that cannot be broken down into constituents.
-
A set of grammar rules that define how symbols are combined together
to make legal sentences of the language.
-
The rules are of the general form
non-terminal symbol -> list of zero or more terminals or non- terminals
This rule can be read as ``the non-terminal on the left-hand side (LHS) of the rule is comprised of the list of constituents on the right-hand side (RHS) of the rule''
- One uses the rules to recognize (a.k.a. parse) and/or generate legal sentences of the language.
-
Backus-Naur Form (BNF).
-
Other notational variants, such as extended BNF (EBNF).
-
Syntax graphs.
-
All notations commonly used for programming language syntax have the same
expressive power -- all produce context-free syntax
- Context-free grammars are a topic we cover at a practical level in 330, and which you will study more formally in CSC 445.
-
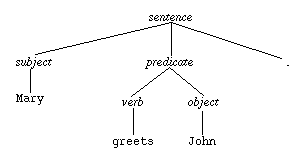
Consider the sentence ``Mary greets John.''
-
A simple grammar that could be used to parse or generate this sentence is the
following:
sentence -> subject predicate . subject -> Mary predicate -> verb object verb -> greets object -> John
-
How do we use the rules of such a grammar to parse or generate a sentence like
``Mary greets John.''?
-
We consider each rule to be a production that defines how some part of
a sentence is recognized or formed.
-
The trace of the application of the production rules can be shown in a tree
form, as in the following:
-
We consider each rule to be a production that defines how some part of
a sentence is recognized or formed.
-
The concept of alternation allows more than one right-hand side (RHS)
for a grammar rule.
-
In standard BNF, rule alternatives are separated by a vertical bar symbol.
-
E.g., suppose we modify the last rule in the above sample grammar to be
object -> John | Alfred
This adds ``Mary greets Alfred.'' to the sentences generatable by the grammar.
-
Another way to extend the expressibility of a grammar is to add additional non-
terminal symbols.
-
E.g., in the above grammar, only ``Mary'' may be the subject, and
``John'' the object; a grammar that removes this restriction would
modify the rules for subject and object as follows:
subject -> Mary | John object -> Mary | John
-
A notationally more convenient grammar to do the same thing adds a new non-
terminal:
sentence -> subject predicate . subject -> noun predicate -> verb object verb -> greets object -> noun noun -> John | Mary
-
E.g., in the above grammar, only ``Mary'' may be the subject, and
``John'' the object; a grammar that removes this restriction would
modify the rules for subject and object as follows:
-
In standard BNF, rule alternatives are separated by a vertical bar symbol.
-
One of the things that makes BNF particularly powerful is its ability to
express languages that have an infinite number of sentences or
sentences that are infinitely (or at least unboundedly) long.
-
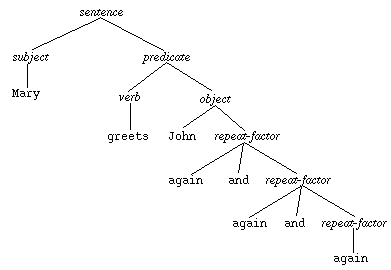
As a first step toward infinite sentences, consider the following modification
to the object rule:
object -> John | John again | John again and again | ...
-
This provides the basic idea of a pattern for generating sentences such as
``Mary greets John.'', ``Mary greets John again.'',
``Mary greets John again and again.'', ``Mary greets John again
and again and again.'', etc.
-
Clearly it's infeasible to write an infinite-length grammar to generate such
sentences. Instead, we notice the pattern that is developing, and use the
following form of recursive notation:
object -> John | John repeat_factor repeat_factor -> again | again and repeat_factor
-
Here is a sample parse tree:
-
As a first step toward infinite sentences, consider the following modification
to the object rule:
- The use of such recursion is a very important part of context free grammars.
-
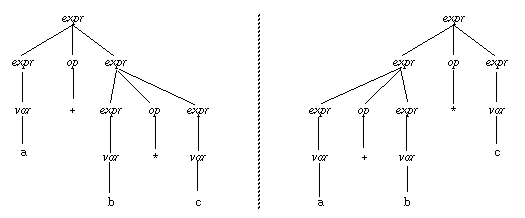
The following is the beginning of a simple expression grammar that fits most
programming languages:
expr -> expr op expr | var op -> + | - | * | / var -> a | b | c | ...
-
From this grammar, we can generate the following two parse trees for the
expression ``a+b*c'':
-
Is there anything wrong with the fact that we can get these two different
trees?
-
First, the syntactic ambiguity is not good; in general we would like a grammar
to give us a unique parse for each sentence.
- Also of possible concern is that the two trees might intuitively be interpreted differently in terms of the precedence of operators.
-
First, the syntactic ambiguity is not good; in general we would like a grammar
to give us a unique parse for each sentence.
expr -> simple_expr | expr rel_op simple_expr simple_expr -> term | simple_expr add_op term term -> factor | term mult_op factor factor -> var | integer rel_op -> < | > | == | <= | >= | != add_op -> + | - mult_op -> * | / var -> a | b | c | ... integer -> digit | integer digit digit -> 0 | ... | 9
-
Here, precedence is represented through a hierarchy of non-terminals --
expr, simple_expr, term, factor.
-
This hierarchy ensures that the operator precedence is properly reflected in
the parse tree for any expression, e.g., that multiplying operators have higher
precedence than adding operators, which in turn have higher precedence than
relational operators.
- Look at things closely here to be sure you understand how this works to define precedence; we will return to this subject in coming weeks.
-
Given the Pascal grammar above, how do we go about parsing a string such as
``a+b*c''?
-
Basically, use the following procedure:
-
Examine each of the symbols in the string from left to right, looking for
grammar rules that we can apply. That is, we look in the grammar for the RHS
of some rule that matches one or more of the symbols at the current place we're
examining in the string.
-
Continuing this process, if we match the topmost rule in the grammar, and there
are no symbols left to examine in the string, then we're done -- we've
successfully parsed the string.
- If we apply the topmost rule, but there are still symbols left in the string to examine, then we've gone too far. In this case, we must undo the most recent rule we matched, and go back to step 1.
-
Examine each of the symbols in the string from left to right, looking for
grammar rules that we can apply. That is, we look in the grammar for the RHS
of some rule that matches one or more of the symbols at the current place we're
examining in the string.
-
Given this procedure, consider how the following parse tree would be derived
from the string along its frontier:
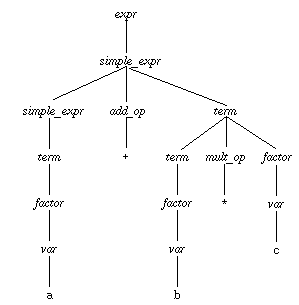
- Note that the simplistic procedure given above is really far too vague to be used formally for parsing. In upcoming lectures and assignments, we will delve much further into how parsing is performed.
-
Extended BNF (EBNF), with the following notational features:
-
A specialized bracketing notation { ... }* is used to express
repetition, avoiding the need for recursive rules in many cases.
-
E.g.,
means a number is comprised of zero or more digits.number -> { digit }* -
This can be expressed with the slightly more complicated recursion:
Note the empty alternative at the beginning of the RHS; this allows for the zero case.number -> | digit | number digit
-
E.g.,
-
Another form of brackets `[' ... `]' express one-of selection. E.g.,
means that a signed number is a number preceded with a plus or minus sign.signed number -> [ + | - ] number
-
One more EBNF construct is the opt subscript, used to indicate an
optional construct. E.g.,
means that a signed_number is a number preceded with an optional plus or minus sign, i.e., by a plus sign, a minus sign, or neither.signed_number -> [ + | - ]opt number
-
A specialized bracketing notation { ... }* is used to express
repetition, avoiding the need for recursive rules in many cases.
-
Syntax graphs.
-
Syntax graphs are a graphical variant of BNF with the following notational
conventions:
- The name of the graph (on the left) depicts the LHS of the rule.
- RHS non-terminals are enclosed in oval graph nodes.
- RHS terminals are unenclosed graph nodes.
-
Graph edges depict rule structure:
- left-to-right flow depicts RHS ordering
- split edges depict alternatives
- looping edges depict repetition
- For example, Figure 2 is the syntax graph for the expr grammar given above on Page 6 of the notes.
-
Syntax graphs are a graphical variant of BNF with the following notational
conventions:
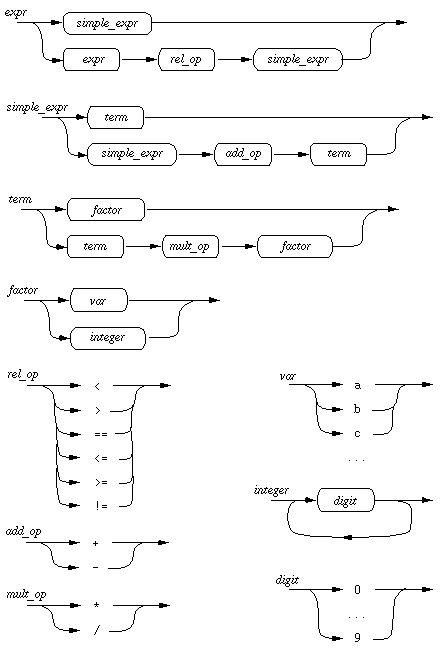
Figure 2: Syntax graph for expression grammar on Page 6.
-
A classic case is that of the ``dangling else.''
-
Consider the following excerpt from a Pascalese statement grammar:
stmt -> assignment_stmt | procedure_stmt | if_stmt | ... if_stmt -> if bool expr then stmt [ else stmt ]opt
-
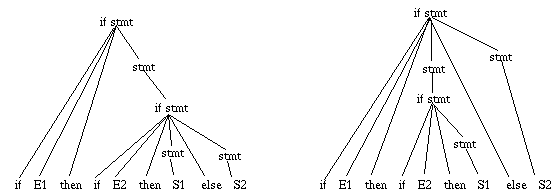
Now consider the statement ``if E1 then if E2 then S1 else S2''.
-
Question -- does the grammar indicate with which of the if's the
else should be associated?
-
Answer: No, since the grammar allows either of the following parses:
-
So, what should be done about this ambiguity?
-
The grammar can be fixed to remove it (think about how this could be done; see
Section 2.2.1 of the book).
-
The syntactic ambiguity can be left, and disambiguated with a semantic
rule; e.g., with a rule stated in English such as: ``The
else ambiguity is resolved by connecting an
else with the last encountered else-less
if at the same block nesting level'' (C Language Reference
Manual, pg. 223).
- Resolving syntactic ambiguity using semantic rules is a means that is sometimes used in the definition of real programming languages (e.g., C).
-
The grammar can be fixed to remove it (think about how this could be done; see
Section 2.2.1 of the book).
-
Throughout CSC 330, we'll be examining what's good and bad about the syntax of
a variety of languages.
-
We'll see how subtle differences can make a major difference in the usability
of a language.
-
A preview of some interesting advances (or regressions) beyond "Pascal-style"
syntax includes:
-
The C-ification of begin-end bracketing, as in, e.g.,
versus the Pascaleseif (t) { s1; s2 } else { s3; s4 }if t then s1; s2 else s3 ; s4 endif;
-
Allowing semicolons to be optional in most normal cases, as in the Icon
language, for example.
- The advent of syntax-directed editors that help programmers worry less about the picky syntactic details of a program. Such editors are now commonplace in IDEs such as J- Creator and NetBeans.
-
The C-ification of begin-end bracketing, as in, e.g.,
-
Here in 330 we will use BNF as a tool in which to express programming language
syntax; i.e., BNF will be used as a communication tool between humans.
-
We will also use BNF as a form of programming language in a couple of the
assignments, where you will use a language called "Yacc" (Yet another compiler-
compiler) to generate a program that does parsing.
-
We will not address the formal theory of grammars -- this is studied in CSC
445.
- Neither will we address formally the theory and practice of parsing programs using context free grammars -- this is studied in CSC 430.