CSC 330 Lecture Notes Week 10

CSC 330 Lecture Notes Week 10
Motivations for Functional Programming in Lisp

Summary of the types of languages Lisp can be
1. Pure Applicative -- disallow setq entirely, as well as all destructive list operations, and all imperative control constructs (the control constructs are essentially useless without assignment anyway).
2. Single-Assignment -- allow let, but still no setq, no destructives, and no other imperative features.
3. Large-Grain Applicative -- allow setq, and imperative control, but only inside functions; i.e., no free variables in functions, and still no destructives.
4. Imperative -- allow general setq (both local and global), and imperative control, but still no destructives.
5. Nasty Imperative -- allow it all, including destructives.
Review of compelling motivations for applicative programming.
1. Referential transparency, i.e., no side effects.
2. Verifiability.
3. Concurrency.
4. Other techniques for efficient evaluation, including lazy evaluation and memoization.
The definition and implications of referential transparency.
1. Referential transparency means that within a given context, multiple occurrences of an expression all have the same value.
2. This is the essential meaning of "side effect free".
3. Referential transparency has a number of important implications for applicative programs, two of which are the following:
  1. Since a given expression E is never evaluated for its side effects, all instances of E have the same value, and E need only be evaluated once in a given context.
  2. In implementations that support concurrency, non-nested expressions can be evaluated independently, and therefore in parallel.
4. Any use of a data modification operator, such as assignment to a global variable or destructive data modification, violates referential transparency.
  1. This is the case, since an expression with side-effects can easily have a different value in the same context.
  2. E.g.,
```
>(setq z 0)
0

>(defun expr (x) (setq z (+ z x)))
expr

>(defun f (x y) (+ x y z))
f

>(f (expr 1) (expr 1))
5

>(f (expr 1) (expr 1))
11
```
The general benefits of side-effect-free programming.
1. Consider the following session:
```
>(setq x '((a 10) (b 20) (c 30)))
((A 10) (B 20) (C 30))

>(load "setfield.l")
Loading setfield.l
Finished loading setfield.l
T

>(setq y (assoc 'b x))
(B 20)

>y
(B 20)

>(dsetfield 'b "abc" x)
("abc")

>x
((A 10) (B "abc") (C 30))

>y
(B "abc")
```
2. The problem here is that the destructive assignment to the object pointed to by x has an effect that is not directly apparent (i.e., is non- transparent) in the call to dsetfield.
  1. Namely, the value of variable y is changed by the call to dsetfield, even though y is not an explicit argument to dsetfield.
  2. The problems with this type of indirect access are well known to imperative programmers.
  3. I.e., it can be difficult to track down the effects of such indirect access, particularly when several levels of indirection are involved.
Program verifiability
1. The most commonly practiced technique of program verification can be outlined as follows:
  1. Provide a specification of program input, stated as predicate P.
  2. Provide a specification of program output, stated as predicate Q.
  3. Prove that if P is true before the program is executed, then Q is true after it is executed.
2. This verification technique relies critically on the restriction that P is a function of all possible program inputs and Q is a function of all possible program outputs.
  1. Without this restriction, the verification may not be valid, since the proof might not be true for all possible program results.
  2. Given this restriction, it is easier to verify functional programs, since all possible inputs/outputs are easier to identify than in imperative programs that reference and/or modify global or pointer variables.
3. An important element of program verification is that the language in which verifiable programs are written must be formally defined.
  1. In general, specifying such a formal definition involves defining the meaning of each construct in the language.
  2. It is generally easier to specify the formal semantics of a functional language than an imperative language, since the effects of any language construct are more isolated in a functional language.
  3. As an introductory appeal to your intuition in this regard, consider the mini- Lisp interpreter of assignment 6 as a form of semantic definition.
    1. In order to define the operational semantics of imperative constructs, the memory must be "dragged around" everywhere.
    2. In contrast, to define the semantics of applicative constructs, far less manipulation of the memory is necessary.
Introduction to functional concurrency models.
1. Consider the following example
```
>(defun f (x y z) ... )

>(f (big1 ...) (big2 ...) (big3 ...))
```
2. The names big_i are intended to signify costly computations.
  1. Given referential transparency, it is possible to evaluate each of the big computations concurrently.
  2. This can result in clear time savings.
3. Hence, in a purely applicative language, a basic form of concurrency is parallel evaluation of function arguments.
4. Another interesting model for concurrent evaluation of applicative languages is dataflow.
Introduction to dataflow evaluation.
1. In the normal applicative evaluation of an expression such as (a + b) * (c - d), we can view the expression evaluation as a post-order traversal of an expression tree such as that show in Figure 1a.
  
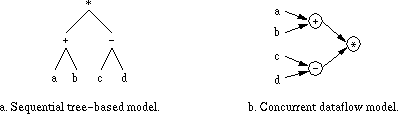
  Figure 1: Two models of expression evaluation.
2. In the tree-based evaluation model, we evaluate using a sequential depth-first traversal of the tree (post-order).
3. In the dataflow model (Figure 1b), we evaluate as follows:
  1. Each operator may execute on its own processor.
  2. Each processor waits for the arrival of its inputs.
  3. Upon arrival of all (perhaps some) inputs, a processor proceeds with its computation, wholly independent of any other processor.
  4. Upon completion, the processor outputs its results, to whatever processor(s) may need them.
  5. The only imposition of sequential behavior is that defined by successive data dependencies, but even this can be partially eliminated with stream-based models.
Introduction to lazy evaluation.
1. The normal evaluation rule in most programming language translators is "eager".
  1. Recall the fundamental rules for Lisp function invocation:
    1. evaluate actual parameters
    2. evaluate the function body
  2. This form of evaluation is eager in the sense that it evaluates all arguments, even if their evaluation may not be necessary.
2. The basic idea of lazy evaluation is not to evaluate an argument until it is actually used in the body of the function.
3. Consider the following motivation for being lazy.
```
>(defun f (x y)
    (cond ( (= x 1) x )
          ( t y )
    )
)




>(f 1 (some-hugely-lengthy-computation))
```
  1. While the function here is not doing anything intelligent, the advantage of lazy evaluation should be clear.
  2. I.e., if the logic of a function body is such that one or more parameters are never used in a particular invocation, then those parameters are never evaluated in that invocation.
4. Can we be lazy in an imperative language?
  1. The answer is no, unless we can guarantee that a segment of imperative code has no side effects.
  2. Consider this example:
```
>(defun g (x y)
    (cond ( (= x 1) z )      ;NOTE: z is free
          ( t y )
    )
)

>(g 1 (setq z 1))
```
  3. In this example, if we're lazy in evaluating argument y, g will not produce a semantically correct result, since z will not be updated.
  4. It is possible to be lazy only in side-effect-free segments of an imperative program.
    1. Specifically, we can perform lazy evaluation on imperative functions or subprograms that can be guaranteed to be side-effect free.
    2. The analysis required to make such guarantees is complicated, but some modern compilers are capable of performing it.
How lazy can we get?
1. In order to make sense out of lazy evaluation, we need to define when we must ultimately perform argument evaluation.
2. In so doing, we need to define what language primitives, if not all, should be lazy.
3. To get started, let's consider the following rules for a lazy Lisp:
  1. cond, cons, car, and cdr are lazy.
  2. All user-defined functions are lazy.
  3. print and all arithmetic/logical operations are eager.
  4. We stop being lazy when an eager function "demands" a value, or when we evaluate a literal constant value (i.e., a literal atom, number, or string).
4. Consider the following example, where "L>" is the prompt for a lazy evaluating read-eval-print loop:
```
L>(defun (lazy+ (x y) (+ x y)))
lazy+

L>(lazy+ 2 (lazy+ 2 (lazy+ 2 2)))
8
```
5. Let us trace carefully how evaluation of the latter expression proceeds.
  1. We start by evaluating the outermost call to lazy+.
  2. Since the first argument is a literal, we go ahead and evaluate it.
  3. Since the second arg is non-literal, we do not evaluate it, but rather proceed to evaluate the body of lazy+.
  4. Within the body of lazy+₁, we find (+ 2 (lazy+ 2 (lazy+ 2 2))).
  5. Since + is eager, it demands that we evaluate both args.
    1. The first arg is trivially a constant.
    2. The second is (+ 2 (lazy+ 2 (lazy+ 2 2))), which we now proceed to evaluate.
    3. This evaluation proceeds just as in steps 1-3 above.
  6. Now we're in the body of lazy+₂, where we find (+ 2 (lazy+ 2 2)).
  7. Again, + demands evaluation, so we evaluate both 2 and (lazy+ 2 2)).
  8. In the body of lazy+₃, we find both args are constant, so (+ 2 2) proceeds without further ado.
  9. At this point, we are ready to unwind the three pending calls to lazy+, since the innermost one has computed a return value. I.e.,
    1. lazy+₃ returns 4
    2. lazy+₂ then returns 6
    3. lazy+₁ finally returns 8
6. While the result of the computation is obviously the same as with eager evaluation (it must be, in fact!), it is important to understand the order in which evaluations took place.
  1. With an eager evaluation of (lazy+ 2 (lazy+ 2 (lazy+ 2 2))), the innermost call to lazy+ would be processed first -- an "inside-out" order.
  2. With lazy evaluation, the order is "outside-in", since lazy+ does not require argument evaluation until it is demanded by + within its body.
Lazy evaluation of potentially infinite functions.
1. An interesting aspect of lazy evaluation is that it can cope effectively with computations that may not compute at all with eager evaluation.
  1. Consider
```
>(defun not-so-stupid-but-lazy (x y)
    (cond ( (= 1 1) x )
          ( t y )
    )
)

>(defun infinite-computation ()
    (prog ()
        loop (go loop)
    )
)

>(not-so-stupid-but-lazy 1 (infinite-computation))
1
```
  2. While the example is again simplistic, the advantage of lazy evaluation should be clear.
2. Another particularly interesting use of lazy evaluation is in the context of potentially infinite generator functions.
  1. Consider the following example:
```
>(defun all-ints () (cons 0 (1+ (all-ints))))
all-ints

>(nth 2 (all-ints))
2
```
  2. Consider the following questions in regard to this example:
    1. What scheme for lazy evaluation could allow the above computation to avoid infinite computation (it may or may not be the same as the scheme we used above for the lazy+ example)?
    2. How exactly does the finite execution of (nth 2 (all-ints)) proceed using a successful lazy evaluation?
    3. What does GCL do with this example?
    4. How would a lazy Lisp evaluator be implemented to allow this example to compute?
Lazy dataflow.
1. Lazy evaluation in a dataflow model is a natural idea.
2. Rather than require that a processing node have all inputs before it begins execution, it can begin as soon as it has enough inputs.
3. A somewhat radical approach to lazy dataflow is fully demand-driven evaluation
  1. All dataflow nodes start computation immediately.
  2. When a node comes to a point in a computation where it needs an input value, it demands it from the node on the other end of the input line.
4. Implementation details of lazy dataflow evaluation can be complex, but the concept is a very interesting one, and it has been the subject of some good research.
Memoization.
1. We noted above that referential transparency implies that any occurrence of the same expression in the same environment need only be evaluated once.
2. Let us consider an evaluation strategy that takes direct advantage of this applicative property:
  1. The first time a function is evaluated with a particular set of arguments, compute the function.
  2. After the first evaluation, store the result for the given args in a table, indexed by the argument values, say by hashing. This is the memo of a function result.
  3. On subsequent evaluations, hash the input arguments, and look them up in the table.
    1. If a value is found for this set of args, simply return it without recomputation of the function body.
    2. Otherwise, compute and store the value for the new set of args.
3. Can memoization be used in imperative languages?
  1. The answer is essentially the same as for lazy evaluation.
  2. That is, memoization can be performed by imperative language compilers where they can guarantee side-effect-free program behavior.
  3. Some production C++ compilers in fact do such evaluation and make use of memoization where possible.
Memoization in dataflow models.
1. There are a number of interesting approaches to memoization in a dataflow model.
2. One intuitively appealing idea is to allow the dataflow lines to remember the most recent datum(a) that passed across.
  1. In this way, the lines themselves perform the memoization.
  2. The computational nodes can reference the line memory, and if a given line has not changed value, the memo'd value can be reused.
To think about.
1. Do lazy evaluation and memoization make sense together in the same evaluator?
2. If so, how?
3. If not, why not?
Some concluding thoughts on functional languages.
1. Even if functional languages are not used much in everyday programming, the concepts of functional programming are extremely influential.
2. For example, compilers for completely imperative languages implement memoization and lazy evaluation techniques, which techniques were pioneered in the study of functional languages.
3. Many so-called "modern" practices of good imperative programming are based on functional programming concepts, including:
  1. Lessening the use of global variables.
  2. Defining variables and function arguments to be constant where ever possible.
  3. Formally specifying program behavior using a functional specification language.
4. Ongoing research in functional languages continues to pioneer new concepts that can be applied to programming and translation of functional and imperative languages alike.