CPE 103 Hashing Lab

Read all directions before your start.

Part 1

Step 1 gives you some test data for this activity, as well as practice with Quadratic Probing.

1. Hash the following keys into a table of size 21 using a hash function of h(x) = x mod 21. Resolve collisions with quadratic probing.
7, 22, 44, 43, 27, 89, 30, 64, 85

Draw a diagram of the completed table.

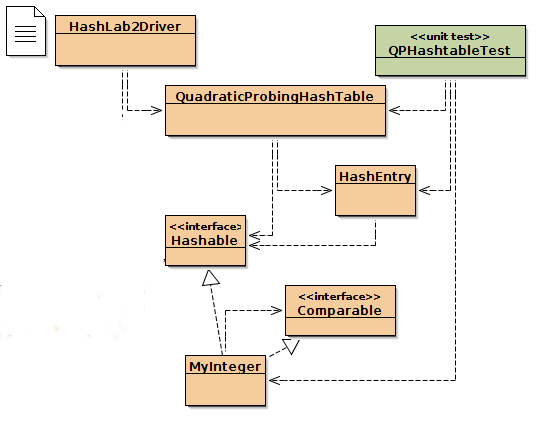
For this activity we are going to study Weiss's implementation of a hashtable.

The following files are needed.  

Hashable.java: Hashable interface

HashEntry.java: Implementation for quadratic probing hash table (entry class)

QuadraticProbingHashTable.java: Implementation for quadratic probing hash table

Comparable.java: Comparable interface for pre-1.2 Java

MyInteger.java: Integer interface for pre-1.2 Java


You may remove the "package DataStructures;" statement at the top of each file.

2. Make sure it compiles and executes correctly.

3. Add a new accessor method, public HashEntry[] getTable() that returns a copy of the underlying array for us to examine. 

4. Write a JUnit test to demonstrate that the program is working correctly. That is, we want to verify that items inserted into the hash table are actually placed in the correct spot in the array according to the Quadratic Probing technique.
Create a JUnit test that inserts the numbers from the exercise above into Weiss's table. Then invoke the getTable() method to obtain the completed table. Write nine assert statements to confirm that each number was placed in the proper location in the table.

5. Convert QuadraticProbingHashTable.java to meet the class coding standards (except the main() method).

6. Add a comment to every logic construct that explains what it does, in terms of the abstraction,
not in terms of Java operations. 

For example,
for( int i = 0; i < key.length( ); i++ )

Don't say "Loops from zero to key length",
Say "Examine every letter in the key."

The goal is that you should thoroughly understand how the implementation operates and accomplishes its tasks.

7.  Run your JUnit tests and verify they still pass.  If not, correct the defects.

Part 2

Warning: These instruction do not tell you everything you need to know to solve this problem. Some details are intentionally omitted; you have to figure these out on your own. Tip: Don't reinvent the wheel. You don't need to write your own hash function.

We will be doing an experiment to determine if the nature of the input data effects the performance of a hashtable.  Begin by modifying the author's Quadratic Probing hashtable class from the previous lab so that it will count the number of probes that are performed to insert an item in the hashtable. An item inserted with no collisions count as one probe. Each spot that collides counts as one probe.

Manually compute the number of probes that should result from the numeric data in exercise 1 above. Run the tests to verify your probe counter is working properly.

Draw a diagram of the hashtable of size 23 that would result from inserting these Strings in the following order: A, W, X, Y, CM, CK, BD, H, MOB, BD. Manually compute the number of probes that should result. (Tip: You can use the BlueJ IDE to assist with this). (Tip: Don't invent your own String hash function. Use the one Weiss includes in his class.) Run your probe counter with this data and verify that it is working properly.

Experiment:
Consider the effect of the following three data sets on the performance of the hashtable:
  1. A common unix word dictionary, in alphabetical order:
    http://www.robblackwell.org.uk/wp-content/words   
    Use the "wc" command to find out how many words it contains.
  2. The text file containing "Huckleberry Finn". Modify the file in a text editor so it has exactly the same number of words as the dictionary file.
  3. A common unix word dictionary, in random order:
    (Tip: The unix sort command has a -R flag to randomly shuffle the input).
Make a prediction based on your theoretical understanding of hashing.  Which would create the most collisions?  Why? 

Now set the capacity of the table to be twice as large as the number of words in the dictionary file.   (Why does this matter?)

Write a driver to run the experiment, hashing all three files and recording the total number of probes. The driver should NOT filter duplicates from the input file. (If "the" appears twice, you should call insert twice.) You might also print the number of words processed, as a confirmation.

Calculate the average number of probes by dividing the total by the number of words.
Do the results match your prediction? Is the average about the same for all input types? If not, which is longer? Explain why.

Submission

Create a document containing your predictions, drawings, exercise results, data collection, analysis, and conclusions. (The drawings may be neatly hand illustrated). Attach your source code and test results (unit and system tests).

References