Graphs: Adjacency Matrix Notation
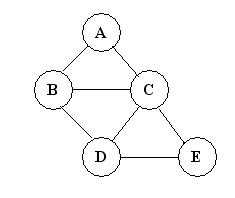
For this unweighted and undirected graph, the adjacency matrix notation
we will use to represent it looks like this:
|
A
|
B
|
C
|
D
|
E
|
A
|
|
1
|
1
|
|
|
B
|
1
|
|
1
|
1
|
|
C
|
1
|
1
|
|
1
|
1
|
D
|
|
1
|
1
|
|
1
|
E
|
|
|
1
|
1
|
|
A representation of an undirected graph
with n vertices uses an n × n
matrix
where the entry at (i,j) is 1 if there is an edge from
vertex i
to vertex j; otherwise the entry is 0. Notice for an undirected graph,
the same entry is placed in both (i,j) and (j,i).
Alternatively, one can use an upper triangular matrix. The rows and
columns are labeled with the vertex identifiers.
The order of vertices does not matter. They are shown here
alphabetically just for clarity.
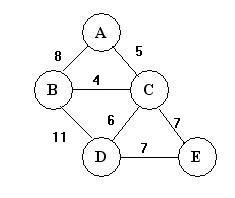
For a weighted graph, we use the weight as the entry, like this:
|
A
|
B
|
C
|
D
|
E
|
A
|
|
8
|
5
|
|
|
B
|
8
|
|
4
|
11
|
|
C
|
5
|
4
|
|
6
|
7
|
D
|
|
11
|
6
|
|
7
|
E
|
|
|
7
|
7
|
|
For a directed graph, each edge is shown only once in the matrix.
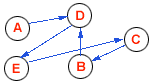
|
A
|
B
|
C
|
D
|
E
|
A
|
|
|
|
1
|
|
B
|
|
|
|
1
|
|
C
|
|
1
|
|
|
|
D
|
|
|
|
|
1
|
E
|
|
|
1
|
|
|
The rows indicates the vertex from which the edge is
leaving, and the column indicates the vertex
to which the edge is entering.


