Boolean Operations on
Triangular Meshes

Katelyn Hicks
CSC 458 - Parallel Programming for Computer Animation
Martin Watt
Spring 2015

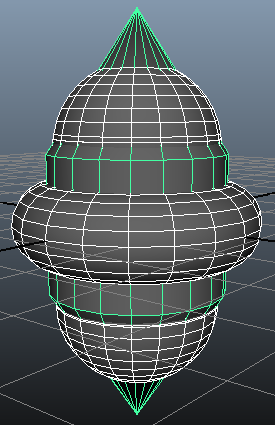
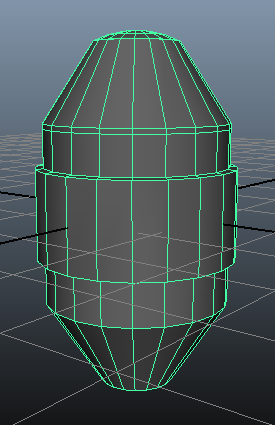
Taking two Maya shapes as input to my program, I found the intersection points between the two triangular meshes. This is one of the first steps for finding the intersecting mesh between the two inputs.

Due to the face that it takes in two meshes, each with a set of vertices and face indices, and checks for an intersection between every face of the first mesh against every face of the second mesh, there is a high arithmetic intensity. The large amount of computation that goes into checking if the meshes intersect and computing the intersecting edge between them makes this problem a great candidate for parallelism.

I used an algorithm that takes in two triangles and outputs whether there is an intersection and the intersecting edge if so (reference below). I used this algorithm and applied it to finding the intersections between the two meshes by checking each face from the first input mesh against the second input mesh. This was parallelized and showed great performance gains (at lease 2x speed for all of the larger test cases).

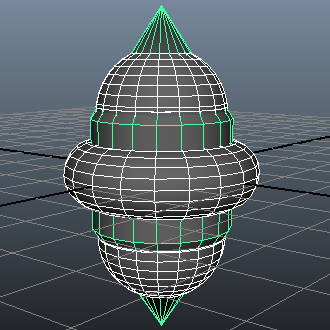
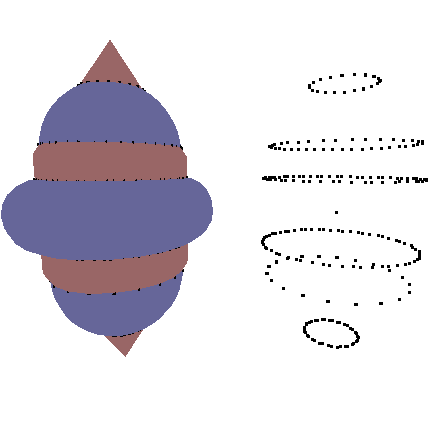
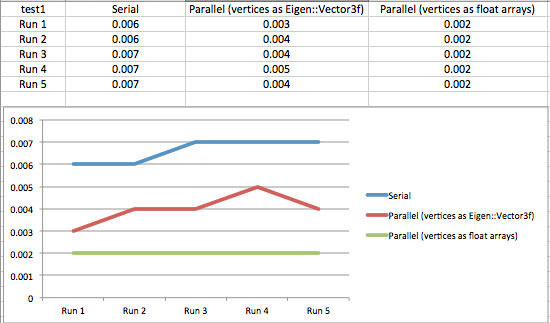
Test 1

Input Mesh 1: 1400 faces, 702 vertices
Input Mesh 2: 124 faces, 64 vertices
Number of intersections: 428
Speedup from parallelism (storing vertices as Eigen::Vector3f): 1.65x
Speedup from parallelism (storing vertices as float arrays): 3.3x

Test1Data

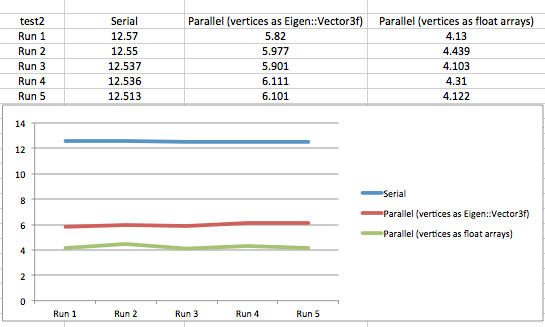
Test 2

Input Mesh 1: 19800 faces, 9902 vertices
Input Mesh 2: 19800 faces, 9902 vertices
Number of intersections: 11708
Speedup from parallelism (storing vertices as Eigen::Vector3f): 2.096x
Speedup from parallelism (storing vertices as float arrays): 2.971x

While this is not a visually interesting test, there are a large number of intersections, it is a great test for how well the algorithm is parallelized for shapes that have many intersecting faces.

Test2Data

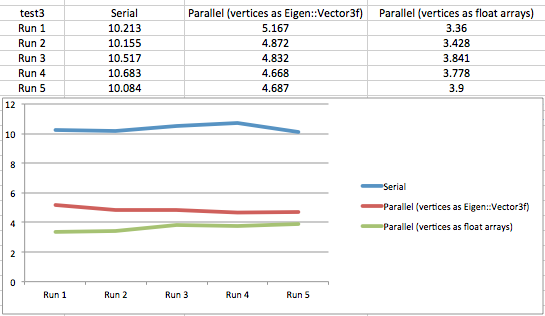
Test 3

Input Mesh 1: 8400 faces, 4202 vertices
Input Mesh 2: 37800 faces, 18902 vertices
Number of intersections: 2021
Speedup from parallelism (storing vertices as Eigen::Vector3f): 2.132x
Speedup from parallelism (storing vertices as float arrays): 2.821x

Test3Data

Future Work

Due to time constraints, I was not able to create the full intersection mesh from the intersecting edges produced by the algoithm. Using these intersections, if I had more time I would have used them for re-triangulating the mesh and creating the new mesh.

I would also continue to try and optimize this algorithm through vectorization. I attempted to try and vectorize the algorithm, but the optimization report showed that each attempt I had at vectorizing was ignored, even with "#pragma simd" due to vector dependence. I took many steps to try and fix these dependencies, but it continued to report this issue in other parts of the algorithm. In order to vectorize this program, it seemed as through a complete refactoring of the code was necessary. This was not feasible for the time I had to complete the project, but would be interesting to see what performance gains would be possible if so.

Offloading to the Xeon Phi would be another goal I would set if I had more time. Once I refactored the algorithm and tried to offload it to the Phi, I found that it caused a seg fault. Investigating the reason for this problem would be my first step towards offloading if I had more time. Then once I found the reason for the problem, I would work towards seeing if this algorithm has a high enough arithmetic intensity to scale well on the Xeon Phi.

Despite a lot of time spent researching how to do this, I was not able to use vertices and their face indices to create a new mesh in Maya. I had a hard time figuring out how to create a Maya plugin that has an input of two meshes and outputs a new mesh. Researching the Maya API on how to export a new mesh would be another part of my future work if I continued with this project. Due to very little experience with the Maya API, I believe that this is the most difficult task of creating the intersecting mesh.

References