A fractal is a “curve or geometric figure, each part of which has the same statistical character as the whole” [1] that is represented by a complex equation. Because these equations are infinite and so complex, it would be impossible to represent them at a set of vertices. One technique that is used to circumvent this problem is ray marching using distance estimator formulas. Put simply, this technique works by calculating the distance from the current pixel to the boundary of the fractal set. [2]
"Classic raytracing shoots one (or more) rays per pixel and calculate where the rays intersect the geometry in the scene.” [3] Ray marching uses a similar technique, but because the geometry in the scene is not defined by a set of vertices, we must use a different technique to find intersections. We march along the ray, each time using a distance estimator function to see how far we are from the fractal set. Once we are within a specified distance of the set, we stop.
The distance estimator will be different for each fractal. Although it is important to understand these functions, we did not write these ourselves. To understand the concept of these distance estimators, it is important to understand that the fractals (or at least two of them) we used are what is called “escape-time” fractals. This means, “we iterate a function for each point in space, and follow the orbit to see whether the sequence of points diverge for a maximum number of iterations, or whether the sequence stays inside a fixed escape radius.” [3]
One fractal we chose to represent is not an escape-time fractal, but rather an iterated function system (IFS) . This complicated term basically means that “the fractal is made up of the union of several copies of itself, each copy being transformed by a function” [4]
The fractals we chose to represent are the Mandelbulb, Mandelbox, and Menger Sponge.
The Mandelbulb is “a three-dimensional analogue of the Mandelbrot set”. [6] In order to understand this complex object, we must first understand the Mandelbrot set. The Mandelbrot set is a 2D fractal represented by the points that do not diverge for the equation zn+1=zn2+c and is pictured below. To arrive at the 3D version of this fractal, the equation is simply changed to zn+1=zn8+c.[3]
 [6]
[6]
The Mandelbox is similar to the Mandelbulb, but instead of an equation of the format zn+1=zn8+c, it is represented using complex operations called folds. Put simply, the algorithm works by using a shape, such as a sphere or cube, and some planes of symmetry. If a point is inside of this sphere or cube, we reflect it across the planes.
As mentioned before, the Menger Sponge is an iterated function system (IFS). In the case of the Menger Sponge, we can construct the IFS using the following steps:
 [5]
[5]
We began our process by using the distance estimator to create a grayscale picture. We used the amount of steps taken in the ray marching to represent a grayscale value. The result:

The next step was to do lighting and shading. The results:

The biggest and most important step was implementing looking and walking around. The results:
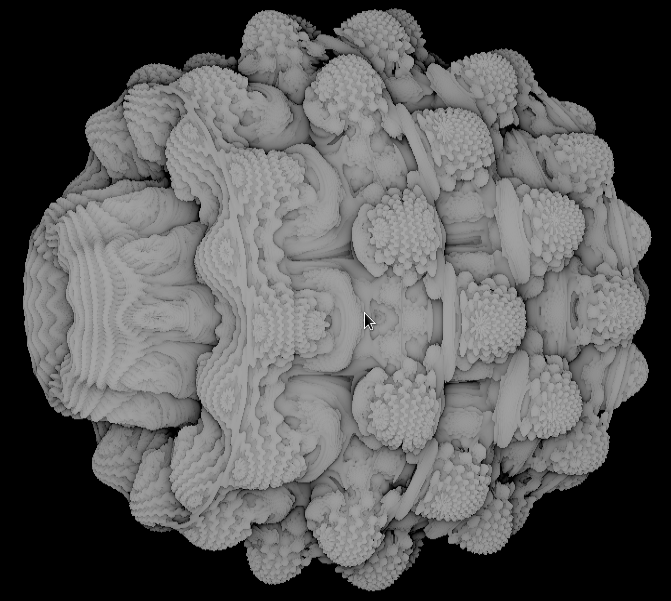
After getting everything else finished, the last step was coloring. For coloring we used a technique called orbit traps, a technique which "keeps track of how close the orbit comes to a chosen geometric object." [3] The results:

Final product for Mandelbox
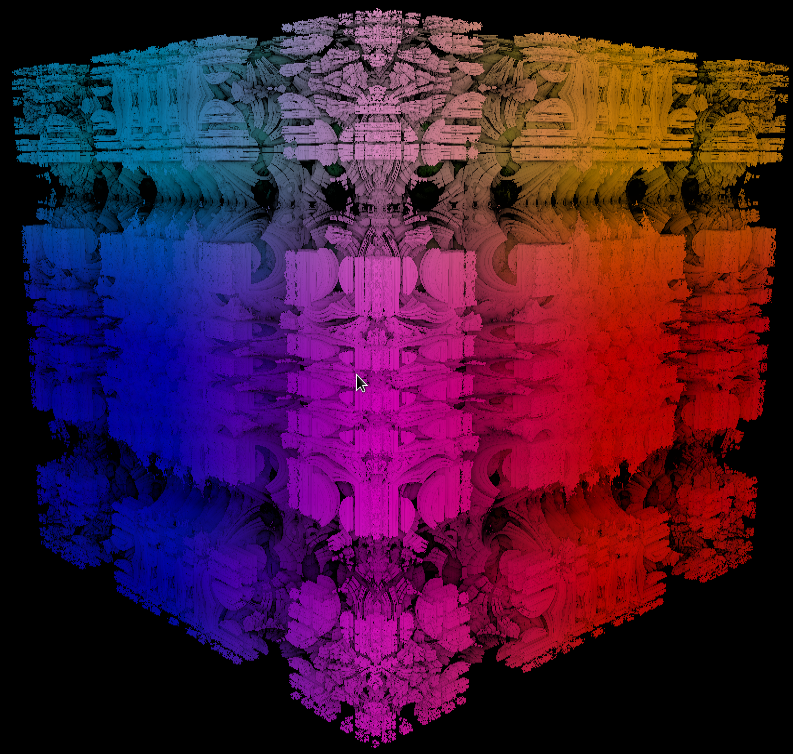

Final product for Menger Sponge:
