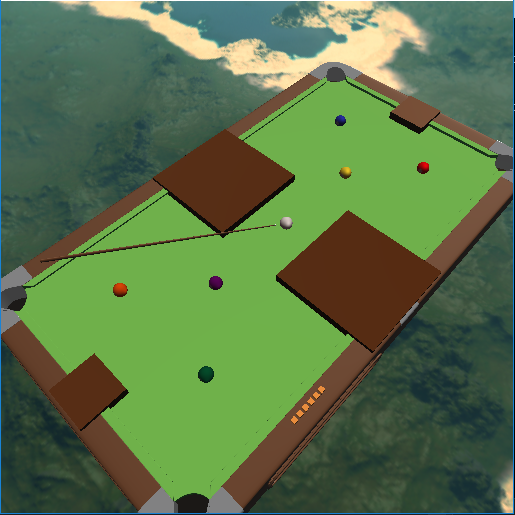
A general-use simulation of a typical pool/billiards table with ball physics. Physics are posteriori, based on idealized elastic collisions, with both horizontal and vertical movement. There are 3 scenarios to play with: 1 standard 15-ball setup, and 2 special setups with added obstacles. The orange tags on the side of the table demonstrate how many balls are still left.
Collisions in the simulation have 2 forms: ball-ball, and ball-block. Ball-ball collisions are purely spherical collisions which are based off of the radii of each ball, and their respective positions. If the distance between the two balls' center points is less than the radius (same for all pool balls) then there is a collision. These collisions can also occur between any pool ball, and the invisible sphere-triggers placed at each hole. The triggers are a workaround for a problem that exists at the corner holes. The ground plane is an axis-aligned rectange, but because of this, the corners stick out somewhat into the corner holes. The triggers check if a ball has entered a hole, and allow it to fall through the ground plane on collision.
Ball-block collisions occur between any pool ball, and a wall or platform. All blocks are axis-aligned, allowing the use of AABB-sphere collisions. For each direction (x,y,z) if the ball's "minimum" and "maximum" positions (eg. x + radius and x - radius) are inside the bounds of the axis-aligned block, there is a collision. Futhermore, if the center of a ball is closer to one side of the block, relative to where it was before moving (per frame), we can determine which side of the block the ball has collided with.

All pool balls have a set of physical properties, although many of the properties are the same considering all the balls are equivalent in shape, size, and mass. At the core, each ball has an acceleration and velocity, and each frame the acceleration is update according to events in the world (eg. hitting the ball). Velocity is then incremented by acceleration, collisions are checked and velocity is chenged if required, and finally position is incremented by velocity. In the y-direction, a constant gravity value is applied to downward acceleration each frame, and if the ball is colliding with the ground, it bounces upward with 50% is original velocity, producing a decaying bounce motion, which quickly evens out to 0 velocity. In the xz-direction, firing a shot adds a set amount (based on how long you charged the shot) to the balls xz-acceleration. Each frame, the xz-velocity is also reduced based on some contstant factor times the ball's current acceleration. This emulates the friction of the table, so that the balls dont roll forever.
If a ball-block collision is detected, the xz-velocity of the ball is reflected along the side which the ball collided with, so it "bounces" off. If a ball-ball collision is detected, it's treated as a perfectly elastic collision and some formulas are run to determine the resultant motion of each ball. The formulas typically involve conservation of momentum, but since p = mv, and the mass of each ball is equal (infinite for blocks) the formula can be simplified to only use each ball's velocity. The rotation/rolling of the balls is handled such that each ball's x and z rotation increments by some set amount every frame, based on their xz-velocity.
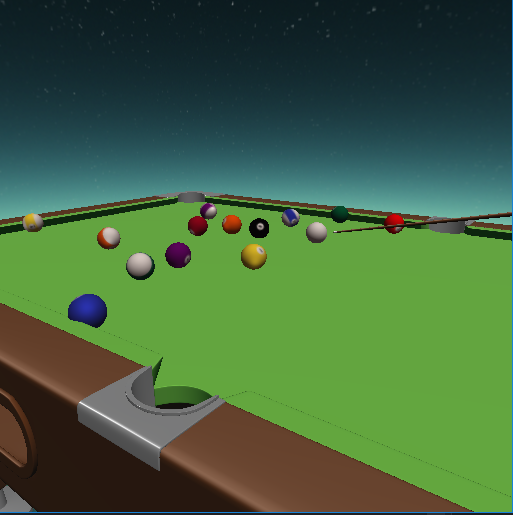
This scenario starts with 3 balls on top of seome raised platforms. Obviously, jumping the ball is required for this scenario but be careful of going over the edge of the table. 5 balls total to score with.

This scenario places two large blocks in the middle of the table, blocking the center holes. Additionally, there are two smaller blocks at the front and back. 6 balls to score with.