GPS Curve fitting

GPS Curve Fitting

CSC 570Q WINTER 2005

Dat Phan

Overview

Application of curve fitting on GPS data acquired from driving.

Purpose of Curve Fitting

For data analysis an infinite data set would be ideal. Since this is not feasible we can model data using curves and interpolate for more data. Because we know the rate of the data is 1hz and that cars gradually accellerate we can create reasonably good curves for interpolation.

Approach

Since the curves are relatively short and straight for data at 1hz it is harder to discern the differences between the different curve fitting techniques. To exagerate the differences I downsampled the data to 1/10hz. After the data is upsampled it can be compared to the original data to gauge effectiveness. To help visualize the data I added a simple color gradient based on velocity between adjacent points.

Description of Data

I gathered data using a Holux GM-210 GPS receiver and GPSd to log positions in longitude and latitude. The GPS receiver updates at 1hz. I used the GPSTk suite to convert those coordinates into [x, y, z] in order to do calculations and to display them using OpenGL.

Linear Interpolation

This is the simplest solution to the least squares problem. Using a the linear equation:

x(t) = (x1-x0) * t + x0

we get a straight line between points. Although this gives a regular interpolation it does not take into account the physics that are occuring. There is no gradual transition between the generated curves.

Cubic Interpolation

Cubic interpolation does a better job of fitting curves because it uses three terms to approximate a curve, instead of just one as with linear interpolation. This is an example of a cubic equation:

x(t) = A * t^3 + B * t^2 + C * t + D

Since Cubic Interpolation takes into account the velocity at each point there is a gradual transition between curves and continuity is guaranteed. However in order to have a good approximation proper velocity vectors are required. When this was implemented the vectors were roughly approximated by taking the difference between the point before and after each point. This gave reasonable curves but they do not fit as well as I had hoped.

Bessel Interpolation

Bessel interpolation fits parabolic curves based on differences between points, and then the differences between those differences. This method does not require vectors but lacks the continuity of cubic interpolation. Still it gives reasonable curves which approximate how a car would behave according to physics.

Yet to be implemented: Bessel Cubic Interpolation

Instead of using the rough approximation method I described before for creating vectors for cubic interpolation, vectors could be defined using Bessel interpolation. Using these better approximated vectors with cubic interpolation would probably give better results than the prior method of cubic interpolation. This would also not have the problem of continuity as with ordinary Bessel interpolation.

Results

Here is the original data set. I drove along Perimeter, back around the dorms, past VGs, south on Grand Avenue, south on US-101, north on Santa Rosa, then turned left onto Highland and then left onto North Chorrow arriving at my house.

This is the same data with the simple color gradient added.

This the data reduced to 1/10hz with the approximated vectors to be used for cubic interpolation

This shows linear interpolation. Notice how each curve does not blend into the next. Also each curve is perfectly straight

Here is the data upsampled using cubic interpolation. Notice how the curves blend nicely into each other. On the freeway section (bottom rung) the curve gets darker than the original, which is not desirable.

Here is the data upsampled using bessel interpolation. The data blends in nicely here as well. The freeway section stays closer to the color in the original than with cubic.

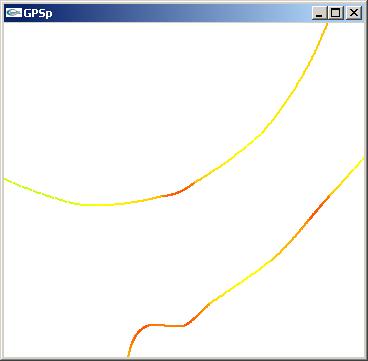
Zooming in on the Bessel interpolation we can see a discontinuity problem in the upper path. The orange part of the path dips slightly then gets back into line.

User Guide

Mouse Usage:

- Right click to access menu.
- Left click and drag in move mode to move view.
- Left click and drag in scale mode to scale view

Keyboard Commands:

B - Toggle curve fitting
V - Toggle Vectors
< - Move single curve back along path
> - Move single curve forward along path
1 - Linear Interpolation Mode
2 - Cubic Interpolation Mode
3 - Bessel Interpolation Mode
- - Decrease Color Gradient
+ - Increase Color Gradient
Q - Exit Program

References

http://gpsd.berlios.de
http://gpstk.sourceforge.net
http://www.topofusion.com/spline.php
http://www.gamedev.net/reference/articles/article914.asp
http://home.att.net/~srschmitt/bessel_interpolation.html