Surface Construction for Hypercomplex Fractals
Jonathan DeKlotz
Final Project for CSC 570q: Computer Graphics
Introduction
While fractals are somewhat of a mathematical wonder, they provide many analogies to the way nature works. Some would argue that they don�t have any direct practical application in math or the sciences. However, fractals continue to inspire and stimulate new ideas in the field of mathematics.
Most people encounter fractals in the form of the 2-dimensional Mandelbrot and Julia sets of quadratic functions. These traditional forms of the fractals are easily visualized in the complex plane (as seen in many text books), but Julia sets of quadratic functions, along with other deterministic fractals, actually exist in higher dimension spaces than the complex plane�hypercomplex space (a hypercomplex number has multiple imaginary components).
My implementation uses quaternions which are four-dimensional. Quaternions are a specific group of hypercomplex numbers having exactly 3 imaginary components. The classic expression i2 �= j2 = k2 = ijk = -1 describes some of the behavior of the imaginary components (i, j, and k) of a quaternion, and is only part of a larger set of algebraic rules associated with quaternions.
Interestingly, the traditional visualization of Julia sets in the complex plane are in fact 2-dimensional slices of the higher dimension fractal. Furthermore, since the fractals exist even beyond 3-dimensional space, it becomes necessary to take 3-dimensional slices of the higher dimension fractal, since [most] humans can�t visualize anything space-like beyond 3 dimensions. The other dimensions may act as parameters that can be varied in a time-like sense.
Current research has provided several mathematically proven distance estimating algorithms for the expressed purpose of visualizing quaternionic Julia sets. Researchers (specifically Dan Sandin and Louis Kauffman) have used iterative distance estimation techniques to ray trace 3D slices of the fractals, providing some very attractive still images and animations (by varying higher dimension parameters or rotating the quaternions over time).
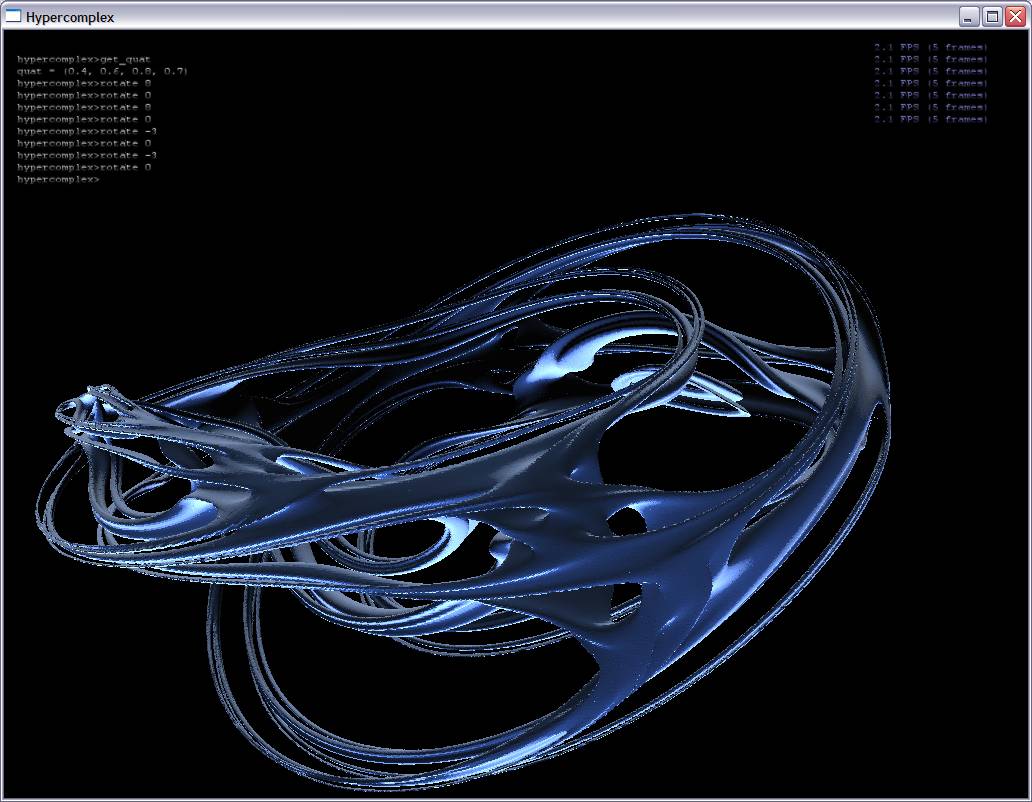
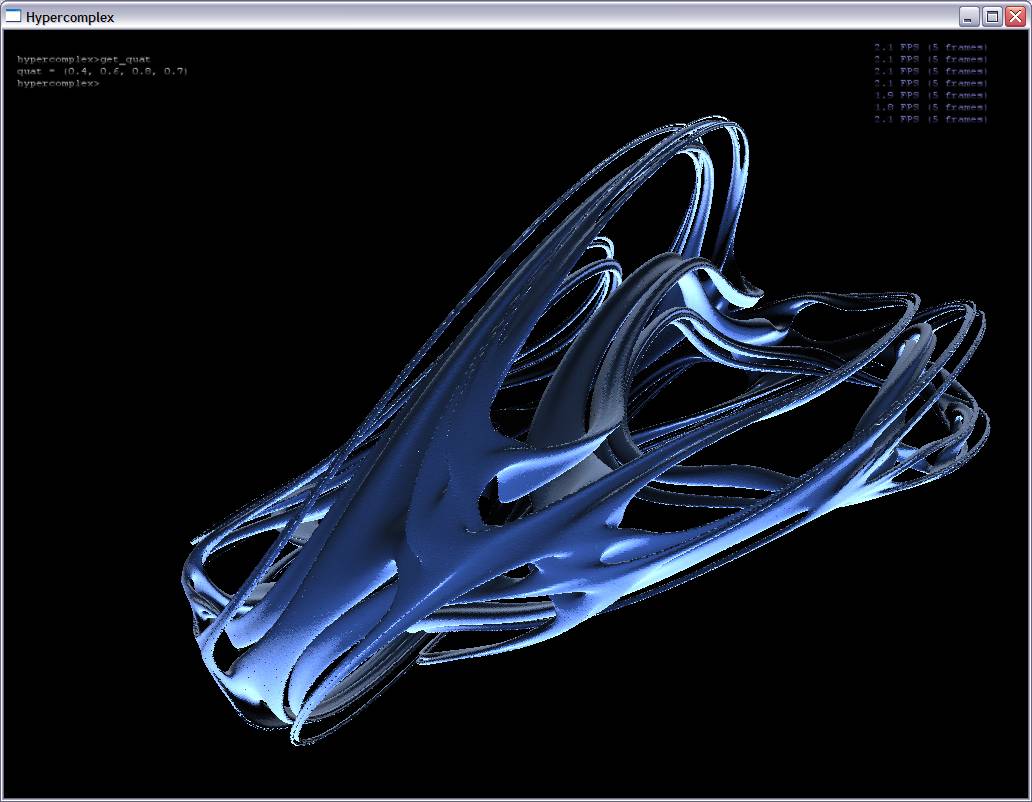
Ray traced visualization inevitably has its pitfalls, which is the motivation for my project: to use proven 3D surface construction algorithms to construct surfaces for hypercomplex fractals (quaternionic Julia sets in my case). I iterate quaternions created from each point in voxel space and an extra point along the fourth dimensional axis. At each point, I can then tell whether or not the point is part of the Julia set. I do this for each point in the voxel grid and then use a simple marching cubes technique to extract the isosurface (see screenshots below).
I have a personal interest in fractals. About five years ago I wrote a simple 2-dimensional fractal explorer program that allowed the user to pan around and zoom in to examine the nature of various fractals and alter the parameters. Recently I stumbled upon a couple of papers by Kauffman on hypercomplex iterations and quaternionic Julia fractals. I was simply intrigued.
Follow this link to see some of my old 2D fractal images:
Screenshots:
(Some of these surfaces have over 2.5 million triangles)


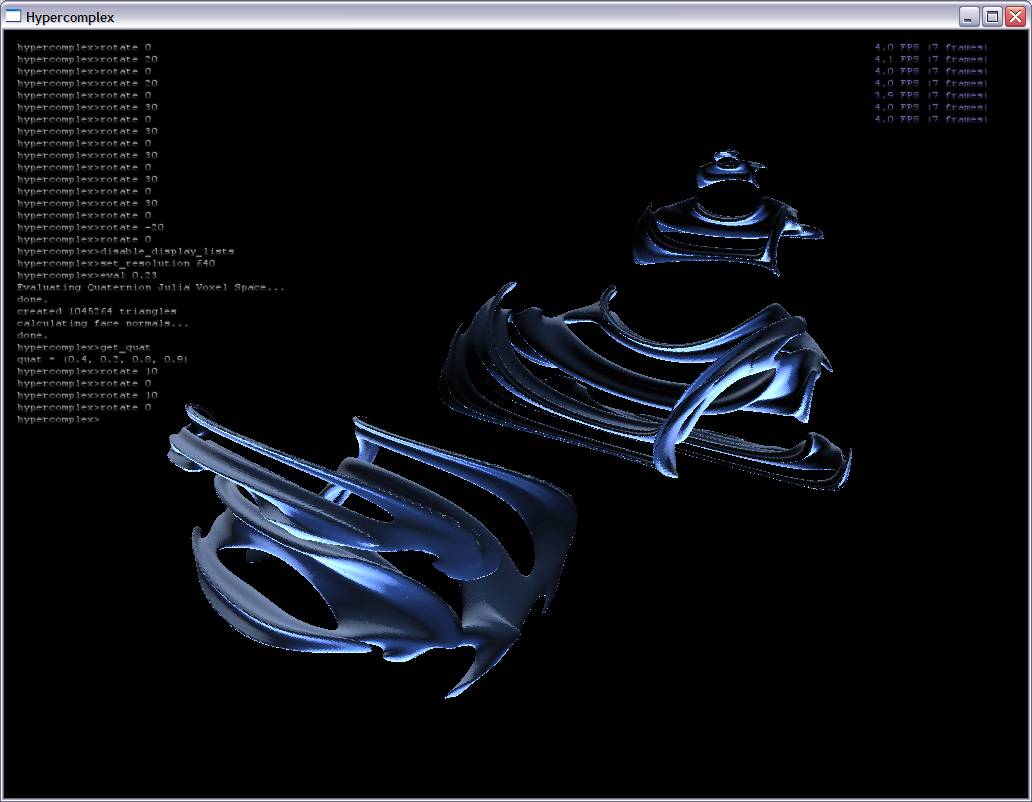
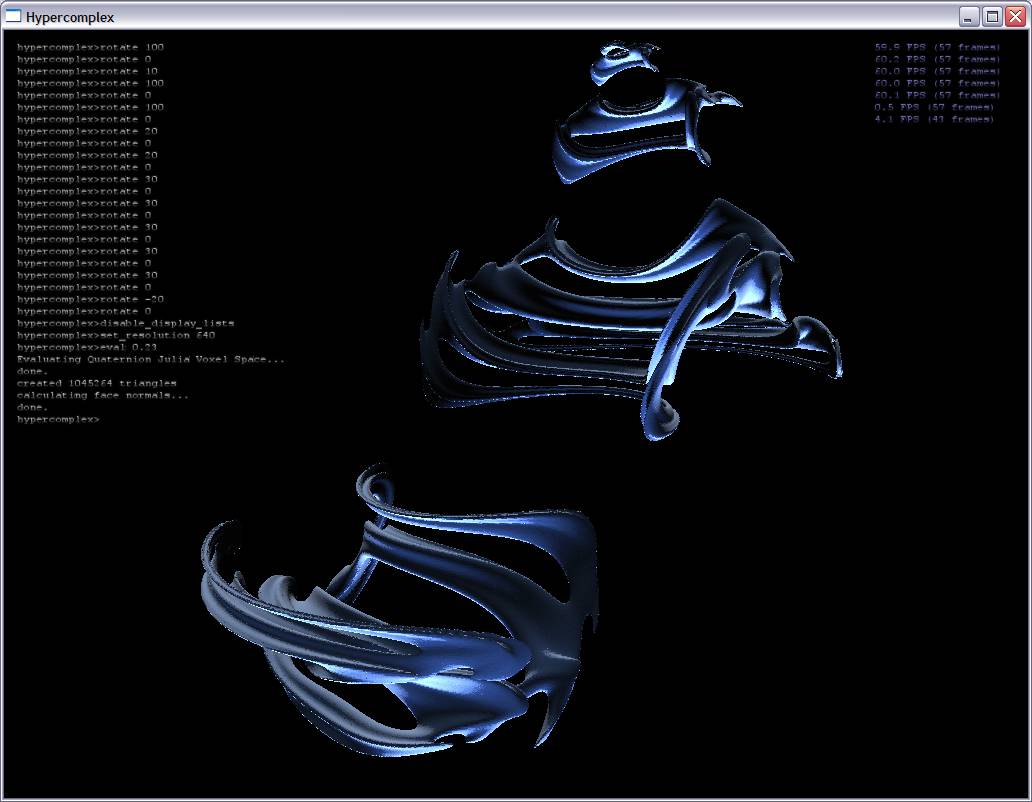



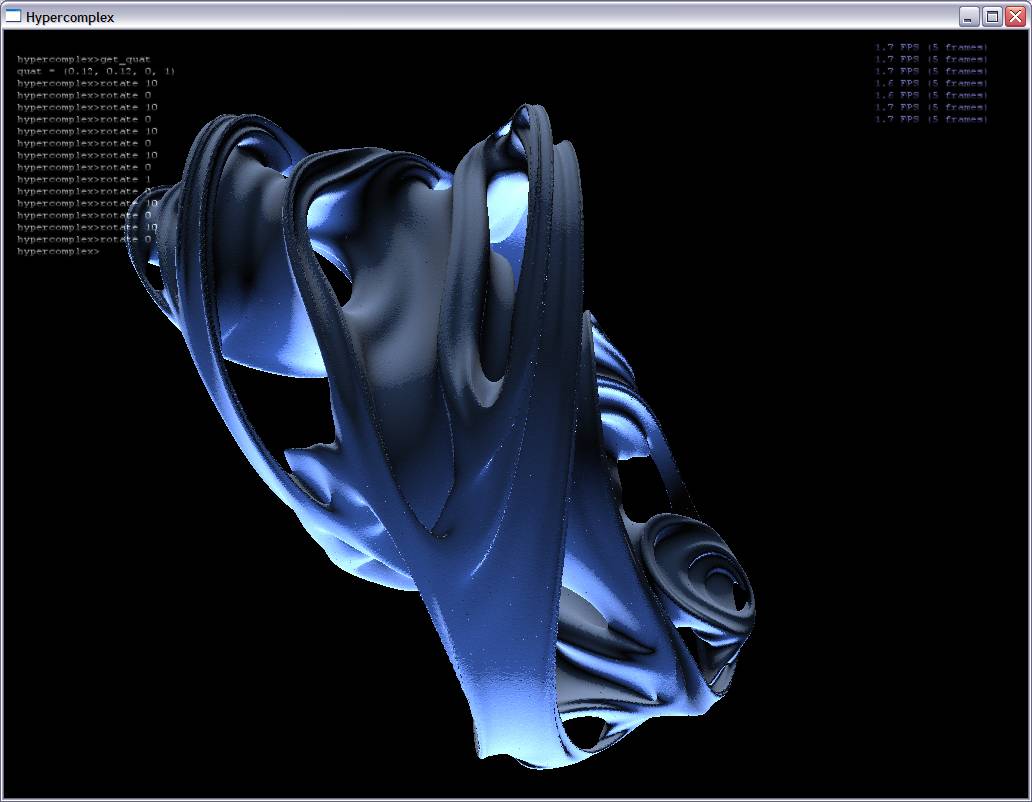
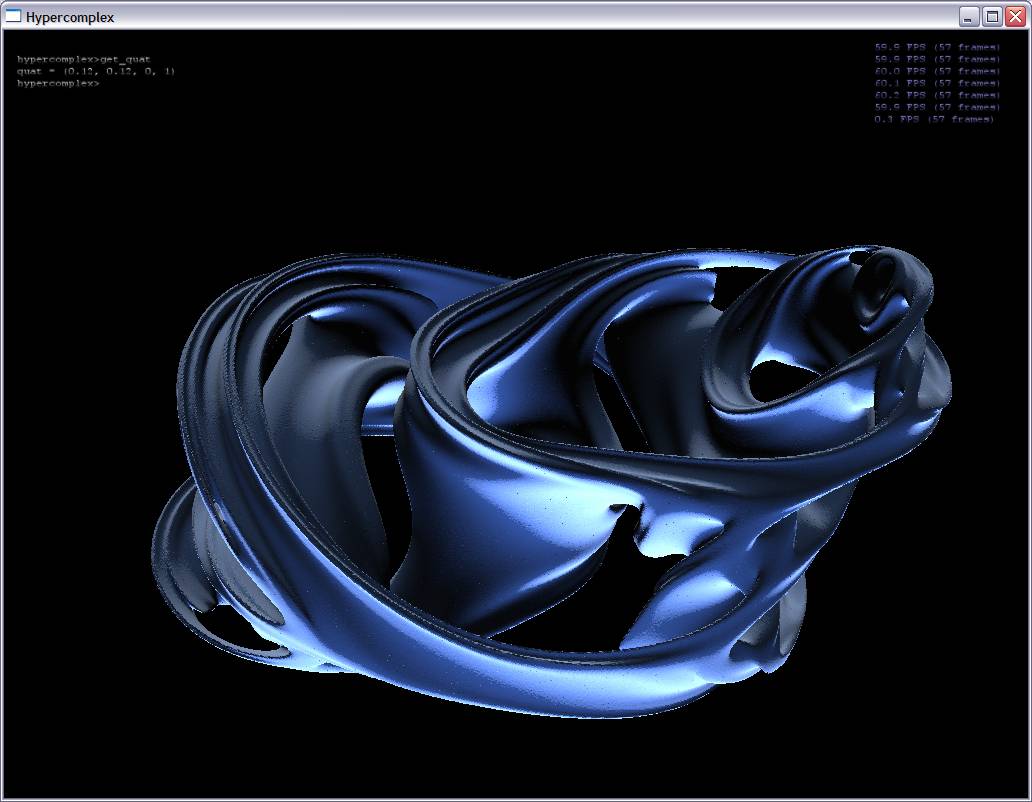
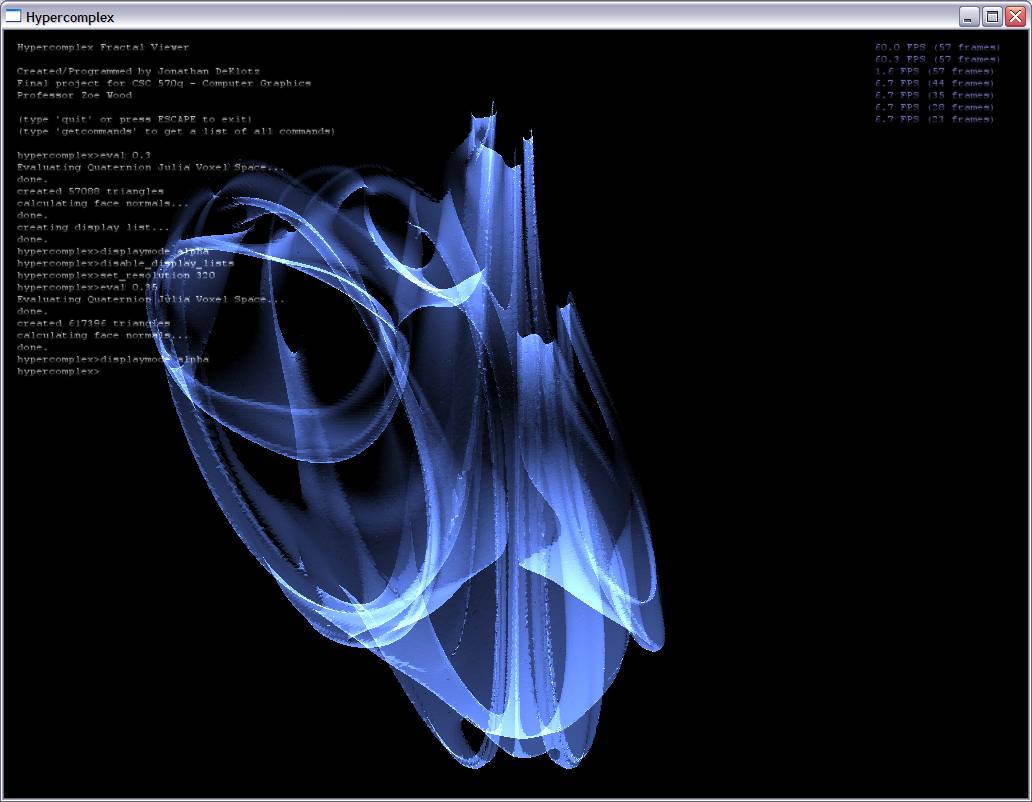
Here are some screenshots with alpha blending turned on:
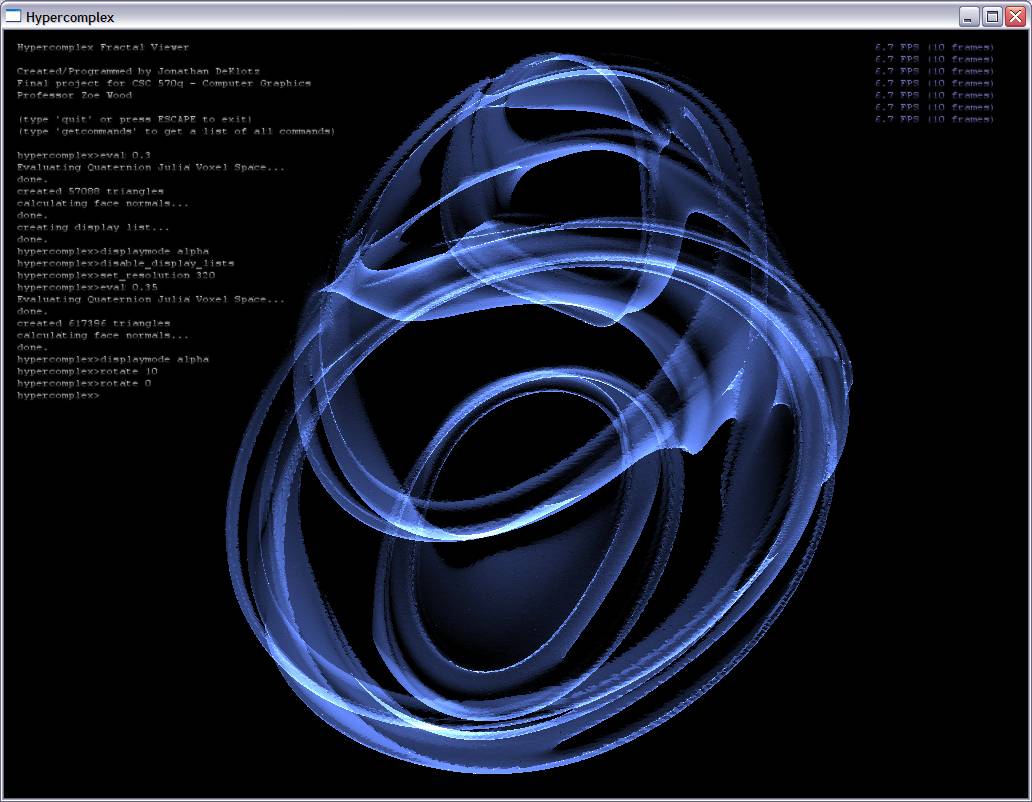
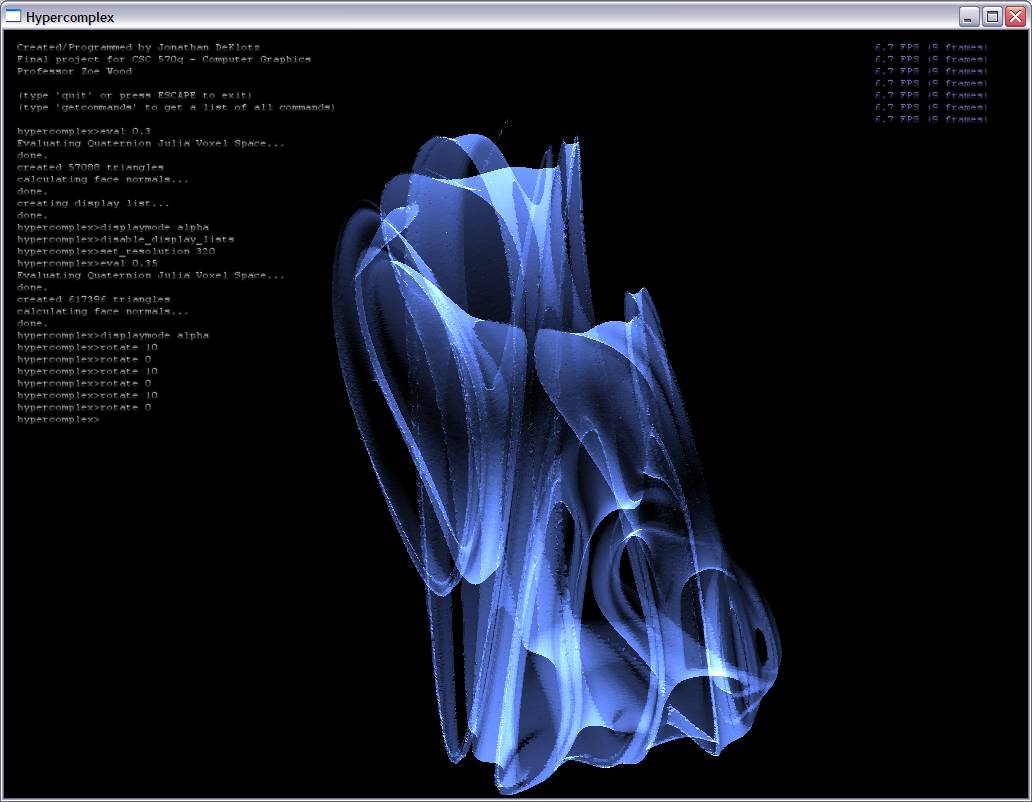
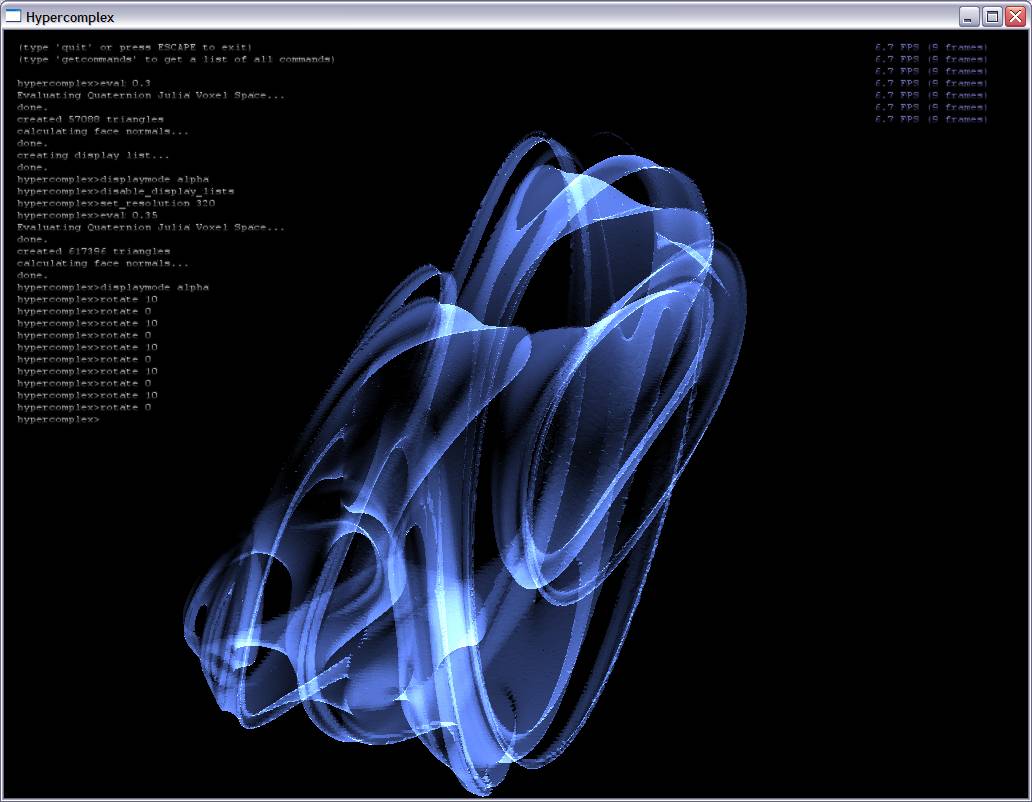
References:
Hypercomplex Iterations, Distance Estimation, and Higher Dimensional Fractals � Yumei Dang, Louis H. Kauffman and Dan Sandin
http://www.evl.uic.edu/hypercomplex/
Shawn Halayka - http://www.oinko1.com/~shawn/