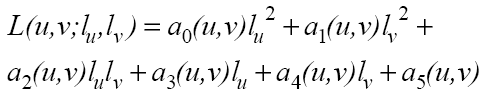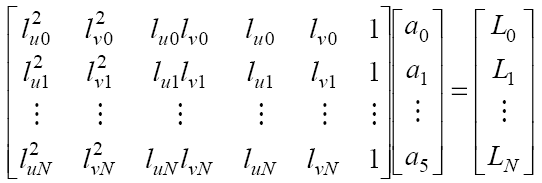Polynomial Texture Maps

570Q Final Project

Jason Rickwald

PTM vs Normal Texture Map

Background

Texture mapping and bump/normal mapping is an easy and commonly used technique for adding detail back to lower detail models. Because of this, graphics card manufacturers have built their cards to make these operations even easier and faster. Texture mapping is typically a mapping of color values onto polygons. Often times these color values are modulated by the flat lighting calculation on each polygon to get a better looking effect. An example of this is the lower portion of the images above. As we can see, simply doing a flat lighting calculation on a texture map made from something that once contained geometry produces a poor result. What we need to do is reintroduce some geometry to correct the lighting calculations. Bump and normal maps allow us to do this. Each texel contains a value that can be used in the lighting calculation to produce a more accurate lighting value for that spot. Using texture maps in tandem with bump or normal maps yields a very convincing result.

Polynomial Texture Maps are a next step in the use of texture maps with normal/bump maps. Typically in a PTM there are nine values stored per texel. The first three are the red, green, and blue chrominance values. The next six values are coefficients to a biquadratic equation seen in [1]. This equation takes a given light position in relation to the texture (project the light vector onto the texture plane), and calculates the luminance for that texel. This function is a simplification of the BRDF for that texel. The final color value for the texel is the chrominance modulated by the luminance.

[1] The Biquadratic:

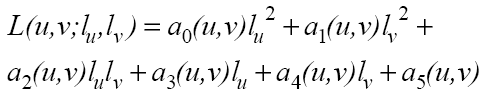
The values in the PTM can be produced artificially to mimic the behavior of bump maps, to produce fresnel effects, to produce anisotropic effects, etc. However, the most interesting use of PTMs is to reproduce real-world data (like the peanuts seen above). A PTM can be constructed from real world data by taking multiple pictures of some texture of interest with a light placed in different positions. The position of the light should be known for each picture taken. Next, we need to fit the biquadratic for each pixel. This is done by first separating out the chrominance and storing that away. The luminance can now be used, along with the known light vectors, to find a least squares fit to the linear system seen in [2]. The matrix of light vector components is unlikely to have an exact inverse (it is unlikely to even be square), so Singular Value Decomposition is used to find a pseudoinverse.

[2] The Linear System:

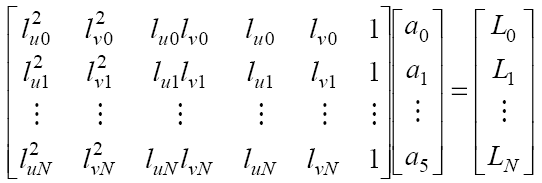
Advantages

HP Labs provides Polynomail Texture Maps, reference materials, a PTM viewer, and a PTM fitter on their website. The first step was to familiarize myself with all of these materials. The next step was to build support for Polynomial Texture Maps into a raytracer that I had built for CSC 471. Once I knew that I could read and display PTMs in a familiar software environment, I was to make a real-time PTM viewer in OpenGL utilizing vertex and pixel shaders. Lastly, if I had time, I was going to try to create my own input data, construct a PTM with it using HP's fitter, then write my own fitter and compare the results.

The Siggraph paper on PTMs, along with a PTM file format description (both available at the referenced website), contained enough information to make the reading and displaying of PTMs in my raytracer a simple task. I won't bother to go into too much detail about how to display a PTM as I have already described the basic principles in the Overview section. I also added a "fake specular" component to my render of PTMs by recovering the approximate normals for each texel using formulas described in the paper. The basic concept to this fake specular is that the normal is directly related to the light position that maximizes the luminance function (note that this is only true for Lambertian materials).

I then set out to write a real-time PTM viewer in OpenGL. The Siggraph paper gives a rough description of how this can be done. Essentially, the PTM can be read in and broken down into three texture maps - one with chrominance values, one with three of the six coefficients, and another with the other three coefficients. Next, a vertex shader is fed the light position, and this is used to calculate the lu and lv components for each vertex (which are then interpolated for each pixel). Lastly, a pixel shader takes the interpolated lu and lv values and texture coordinates, does the appropriate lookups, and does the lighting calculations using the PTM. I wrote my vertex and pixel shaders in Cg, and I again implemented the fake specular mentioned above. I had few difficulties with the PTMs at this point. The most challenging aspect to this part of the project was that I had never written vertex or pixel shaders before. Most of my difficulties, therefore, revolved around quirks with OpenGL and Cg.

With only a few days left before due date, I decided I wanted to undertake the fitting of a PTM to acquired data. The first step was to get some data to work from. HP does not provide the source pictures used to construct the PTMs that they have on their website, nor could I find any other good source pictures online. What I had to do, then, was make my own "good enough" source data. My solution was to prop a camera on a box (trying to keep it as stationary as possible), and shine a flashlight onto my backpack in the dark. For each picture, I did my best to approximate the light position vector. There were six pictures in all, some of which are shown below.

I put my source data through HP Labs' PTM fitter and was surprised how good the result was considering the input data. The output PTM looked the worse when the light was positioned below the backpack, as there was no source data for that area, but looked mostly good in other areas.

The creation of a PTM is outlined in the Overview section above. My fitter program followed the same steps. However, I was faced with two main challenges to be able to implement a fitter. One challenge was how to do the separation of chrominance and luminance for each pixel. The technique for doing this is not described in any of the materials made available from HP Labs. The technique that I settled on (which is possibly incorrect) was to take the average value for the red, green, and blue components for each pixel and store that as chrominance. Then, for each pixel, the luminance value for each of the N images was the value that best fit the system of equations:

For each pixel, we can now construct the linear system [2] seen in the Overview section. Actually, the Singular Value Decomposition of the light component matrix is calculated before hand for the entire set of images. It is then used for each pixel to fit coefficients.

This brings me to the next major hurtle - Singular Value Decomposition. The paper mentions that this is how a least squares solution to the system is solved, but I had never worked with the SVD for a matrix before. I looked up Singular Value Decomposition in my Linear Algebra textbook (referenced below) as well as in a number of online sources, and I got a pretty good idea of the concepts behind it, how it could be done, and how it could be used to find a least squares solution to a system of equations. However, all of the sources I found warned that the methods presented were good for learning the concepts and for doing hand calculations, but they did not translate well to a machine environment. After some more research online I found a fast and stable implementation of an SVD algorithm presented in Numeric Recipes (referenced below). This algorithms seems widely used and adapted, so I felt safe using it in my fitter. If I should not be using it, I will happily remove it.

I have made two versions of the fitter program. The first version that I started on would produce LRGB PTMs. However, I was encountering numerous bugs that I was having a difficult time tracking down. To simplify the problem I started a second version that was almost identical to the first except that it produced RGB PTMs -- removing the need to separate luminance and chrominance. Once I had fixed the bugs in the RGB version, I went back to the LRGB version and completed it. If I had more time, I would merge the two programs and let the user specify which format at the command line.