Mesh Simplification using Quadric Error Metrics

California Polytechnic State University, San Luis Obispo

Jeremy Seeba

What are Quadric Error Metrics?

Quadric Error Metrics are a measurement of error that determines how far a vertex is from an ideal spot.  Each individual quadric is found using the plane equation derived from a triangle.  The normal of the triangle sets the orientation of the plane and one of the vertices in the triangle is used to find the offset.  The plane equation is ax + by + cz + d = 0 where a2 + b2 + c2 = 1.  The quadric Kp expressed in terms of a, b, c, and d is:

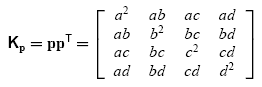
Quadrics are associated with vertices and every applicable quadric is added to a vertex.  Before any mesh simplification happens, a quadric or set of quadrics associated with a vertex will evaluate to 0 if the vertex location is evaluated using the quadric.  Vertices are evaluated against a quadric by multiplying the transpose of a vertex with the set of quadrics then with the vertex again.  Evaluating the following function gives the error:

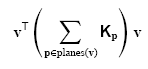
The quadrics are observed to be symmetric therefore only 10 numbers instead of 16 need to be stored.  When an edge is collapsed, the quadrics should be unioned but as observed by [1], addition may add some imprecision but the benefits in terms of speed outweigh unioning the quadrics.

The algorithm (from [1])

  1. Compute the quadrics for all initial vertices.
  2. Select all valid pairs.
  3. Compute the optimal contraction target for each pair.  The error of the combined quadrics of the vertices in the pair are evaluated at the optimal contraction target to find the cost of contracting a pair.
  4. Place all the pairs in a data structure sorted by minimum cost.
  5. Iteratively remove the collapse pair and repeat step 3 with all edges that were affected by the collapse.

Computing the optimal contraction target for each pair is done by inverting part of the quadric matrix:

My Program

My program is almost an exact implementation of the algorithm described in [1].  It is implemented in OpenGL.  It can take input from and can output to a simple mesh format which defines vertices and faces by listing "Vertex [id] [x] [y] [z]" and "Face [id] [vertex id 1] [vertex id 2] [vertex id 3]".  The number of target faces in the simplified model can be set.  The display mode can be set to points, edges, or shaded faces. 

Keys:

bullet 'l' - prompts for filename to loads a mesh to be simplified
bullet 'f' - prompts for a target number of faces in the simplified mesh
bullet 's' - begins simplification
bullet 'w' - prompts for filename to write a simplified mesh
bullet 'd' and 'D' - changes the display mode up and down respectively
bullet '\' - toggles alternate visualization when displaying edges or faces
bullet '+' and '-' - changes the alternate visualization of the edges
bullet 'n' - toggles shading of faces from flat to average of all touching triangles

The mouse controls rotating the mesh by clicking and dragging with the left mouse button.

Screenshots

Dragon model simplified to 2500 faces from 10000 faces.

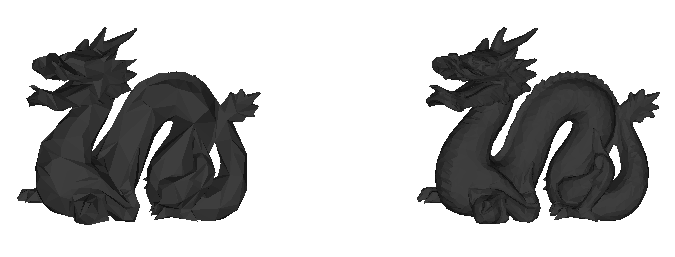
The same image displayed with faces shaded.

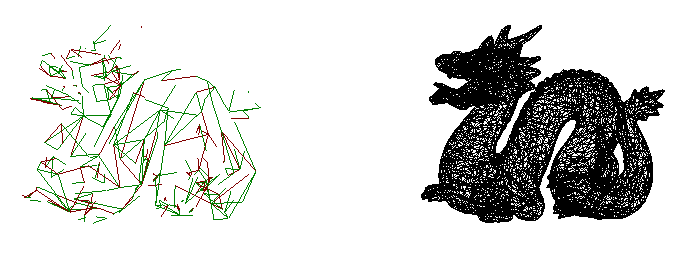
The same model simplified to 1500 faces and displayed using the alternate edge visualization.

bullet Green edges can't be collapse because it would cause a normal flip on one of the surrounding triangles. 
bullet Red edges can't be collapse as they fail the one-ring manifold test. 
bullet Blue edges can't be collapse because they fail the sharkfin manifold test.

The following is a series of simplified models from 10000 to 1000 shown in different display modes in 1000 face increments.

Results

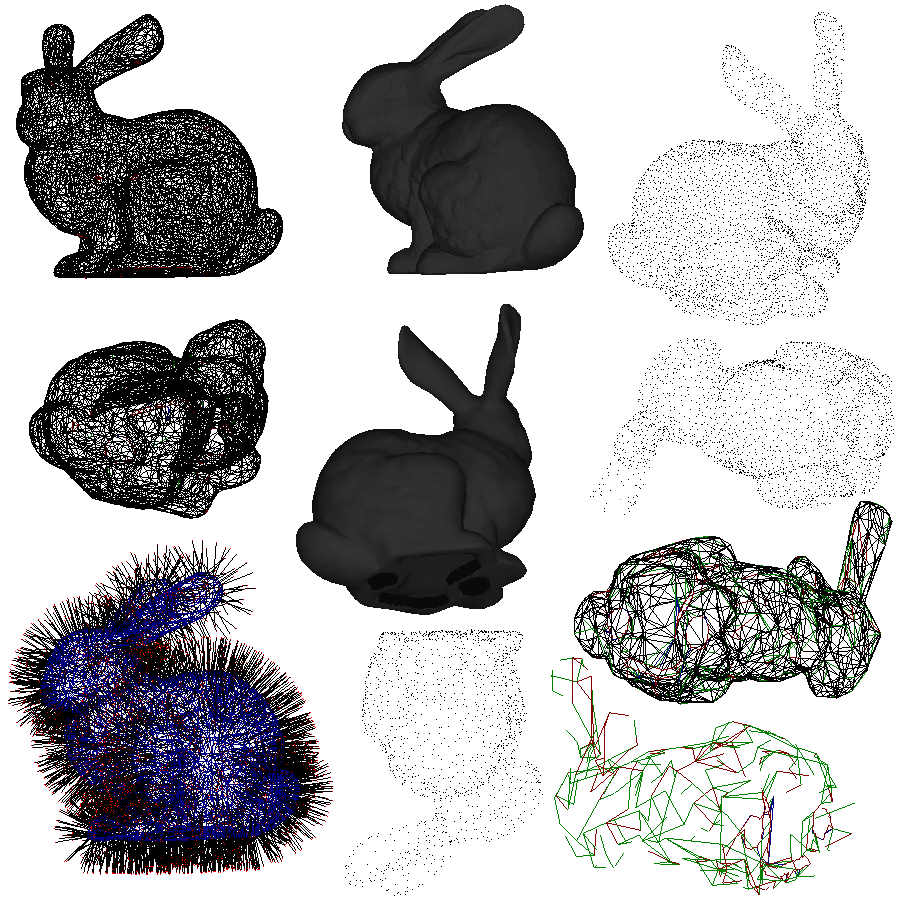
I am very happy with the results of simplification.  The simplification for meshes that are around 10,000 to 20,000 faces is very quick.  The final results resemble the initial mesh very closely.

Future Work

bullet Implement unioning of quadrics instead of adding to make the simplification more accurate.
bullet Optimize program to speed up simplification of larger meshes
bullet Work on the User Interface to make the program more intuitive
bullet Handle inputs from other types of file formats (ply, etc)
bullet Anything I can think of if I have the time

[1] Garland, M. and Heckbert, P. S. 1997. Surface simplification using quadric error metrics. In Proceedings of the 24th Annual Conference on Computer Graphics and interactive Techniques International Conference on Computer Graphics and Interactive Techniques. ACM Press/Addison-Wesley Publishing Co., New York, NY, 209-216.