The purpose of this project is to use known information about materials, camera position, and lighting to acquire 3D information from a single image. There are several methods currently in place to acquire 3D information from a 2D image but they are limited by a number of constraints. This method, while still rather constrained, has different limitations from other methods.
The most popular methods for capturing 3D data use a projector and a camera to compute range data. These methods are limited to small objects and require substantial prep time to align both the projector and camera accordingly. The method proposed in this paper eliminates the need for a projector and could be expanded to acquire data from larger scenes such as architecture.
The method proposed uses known light vectors and viewing vectors, and known object material to compute normals for a surface. You can then use these computed normals to reconstruct the shape of the object. This method may be limited to only acquiring data for objects with consistent material but this may be overcome with preprocessing of the image.
The primary goals of this project are to determine the feasibility of this method. The steps to achieve this goal are.
Similar work to the method proposed has been done and will provide performance comparisons for later versions implementations of this method.
Previous algorithms that compute shape from shading have either used a complex mixture of computed parametric surfaces, gradients, Sudo-Inverses of matrices, or multiple light sources to compute the shape of an object from the shading in one or more images. The "Shape from Shading" algorithm that Corlotto describes uses information shadding to directly compute depth but is limited to wide light angles and extremely simple shapes such as spheres and cones.
The algorithm proposed uses a single light source and a single image to compute the shape of an object. We start by first computing the normals for every pixel on the surface, then computing the shape of the surface.
The most basic shading of a lambertian surface can be computed by taking the dot product between the light vector and the normal. The equation is as follows:
I = L▪N Where I is the final intensity of the pixel (known), L is the light vector (known), and N is the normal (unknown)
If we multiply out the dot product we get this:
I = L x*N y + L x*N y + L z*N z
Knowing that the normal N is of unit length we can solve for one of the components by simply using the pythagorean theorem leaving us with this:
I = L x*N y + L x*N y + L z*√(1 – N x 2 – N y 2)
We now have one equation with two unknowns and have basically solved for a circle of possible normals around a light vector that gives us a solution.
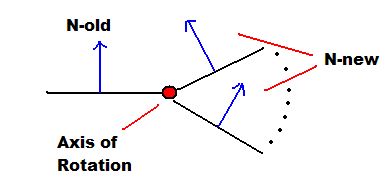
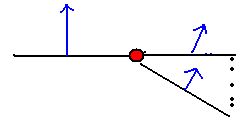
We can further constrain the problem by assuming we know a normal that neighbors the normal we are trying to compute. Getting the position of these neighbors is easy since we are getting the data from a regular grid of pixels. So for any given face we can use a neighbor above, below, or to either side to find a solution.
For example if we are trying to find a normal for face N-new we use the already computed normal to the left of N-new (call it N-old) to constrain the problem to a rotation about a single axis.

We can now compute a N-new that falls within the circle of normals we derived earlier thus giving us our new normal. This is done by computing the difference in the dot products.
I = L▪N = cos(ө)
Φ = arccos(I at N-old) - arccos(I at N-new) where Φ is the angle between the two normals. We then rotate N-old by Φ to get N-new. There is a slight issue of the light source being at infinity and all pixels using the same light vector which we will address later.
Once the faces start pointing in arbitrary directions we can always bring the normal back to a simple coordinate frame by applying a rotation to the normal. This is easily done by converting the normal to polar coordinates, applying the rotation, then converting back to cartesian coordinates.
We can now solve for normals knowing a neighbor so we can start everything off by knowing a single normal then iteratively calculating the neighbors until all normals are computed.
To get the known normal we can either have the user input a normal and the position it corresponds to on the image. Or we can assume that the brightest pixel on the image is at the optimal angle to the light. Which in the case of lambertian surface, this is the direction of the light source. For surfaces with a specular component, the view vector has to be known and the optimal angle is half way between the light and view vectors.
A light position that is infinitely far away from the surface of a model (ex. sun) has the problem of symmetry. Since the light vector is the same for all vertices on a surface there are two possible solutions to the method previously described. Deciding which solution to take can be determined in one of three ways:
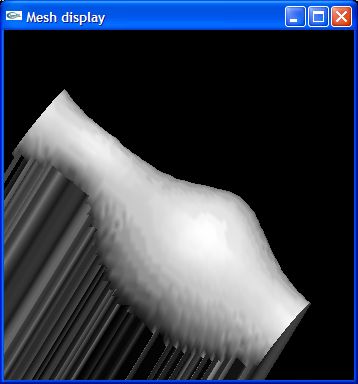
For this version we use the third method of assuming that the object is spherical (this can be seen by an artifact in the results as a crease through the center of the surfaces).
Once we have the normals we can use basic trigonometry and an assumption that the surface is relatively smooth to solve for depth. This can be thought as adjusting the z value of a face untill the face is perpendicular to the normal as shown below.
The implementation was in C++ using OpenGL. The 2D image format is Portable Pixel Map (PPM), a simple format that just stores RGB values for each pixel in the image. The final product is an executable that a user can run on a PPM and the application will create a 3D surface that can be viewed from multiple angles. In all images the light source will be at the same position as the camera.
The algorithm makes three assumptions. First that the material has a very small specular component, second that the material has a very small ambient component. Finally we assume that there is at least one point that faces the cammera.
The executable takes three parameters, image name (ex. face.ppm), and an x and y start point. Since the algorithm uses only one image we have to know at least one normal to start. The x, y pair describe the location of a normal facing the cammera. If an x, y pair is not provided the system will choose one for you by finding the brightest spot on the image (since the light is at the cammera this will be the point facing the camera.
The current version of the program uses incremental approximations instead of computing the normal straight from shading. Although slower, this has yielded better results since computing values straight from the intensity does not always have a single solution creating dead verticies on the image.
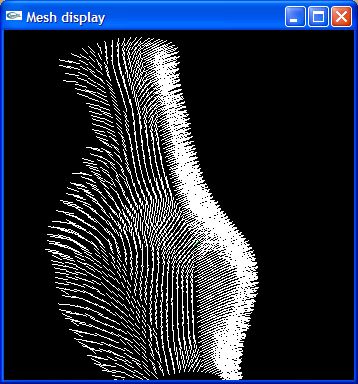
Also the current version scans horizontally when computing normals. Scanning in both horizontal and vertacl directions has been implemented and the resaults were not as impressive (normals were improved, depth was unimpressive). The normals were computed better but the depths were quite a bit off. This will be fixed in later versions by applying various matrix transformations before computing each normal. But for now the concept has been implemented to a point that the concept has proven to work, it just needs fine tuning.
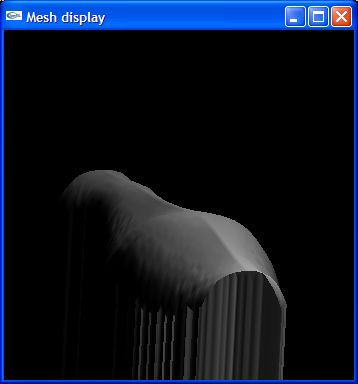
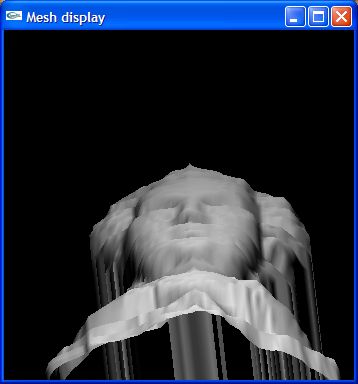
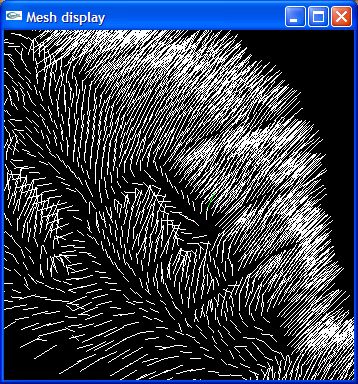
Here are the results of the current implementation of the method described. Expect much more advances as other components of the implementation develope. The screenshots were taken after lighting the surface with the computed normals and NOT with a texture map. The normals for the surfaces are also shown for the Vase and Mossart face.