Vol Pack's Shader
Simple Cosine Shading
Two Smoothing Passes (surface defined by density)
Two Smoothing Passes (surface defined by gradient)

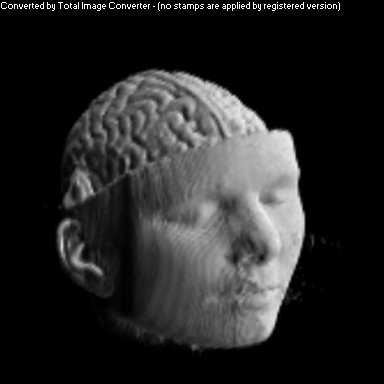
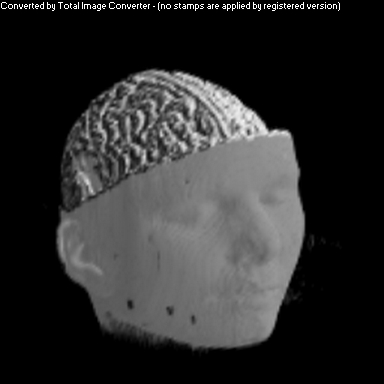

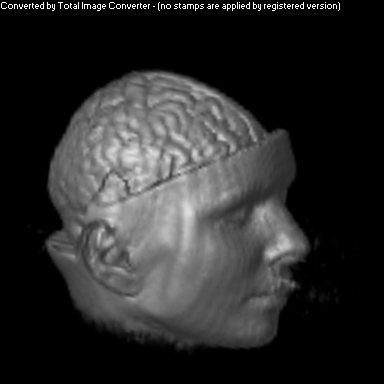
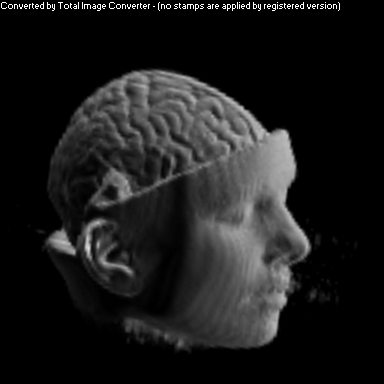
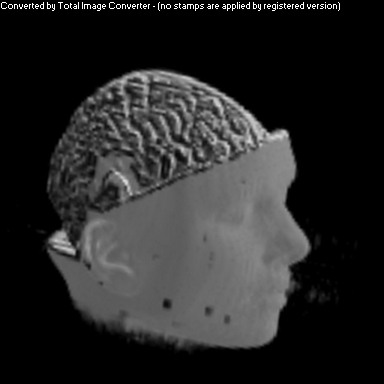
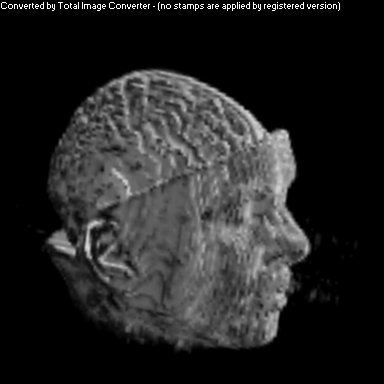
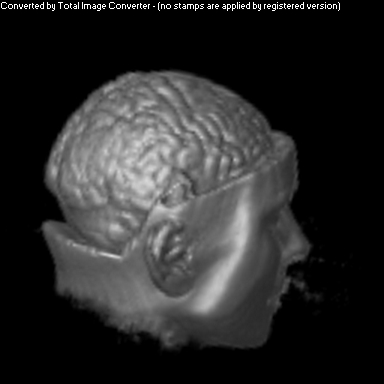
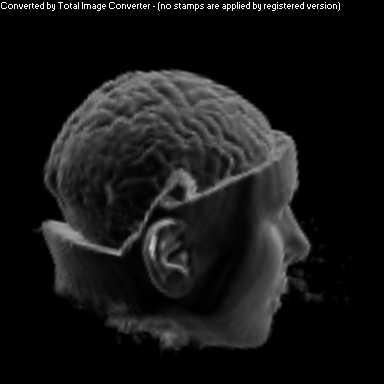
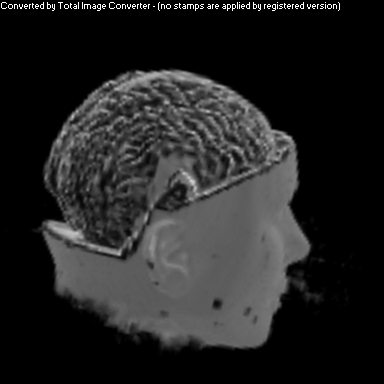
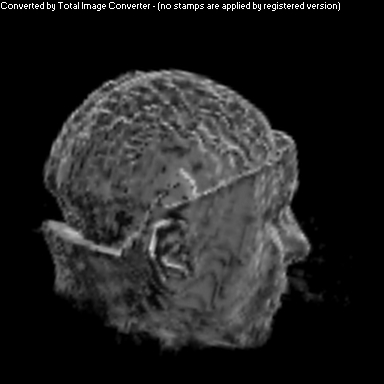
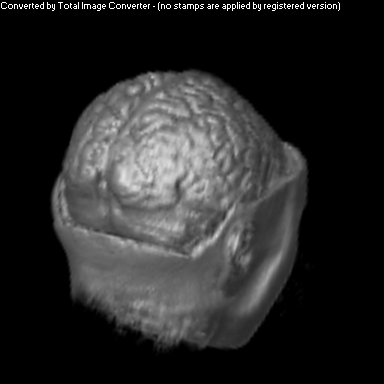
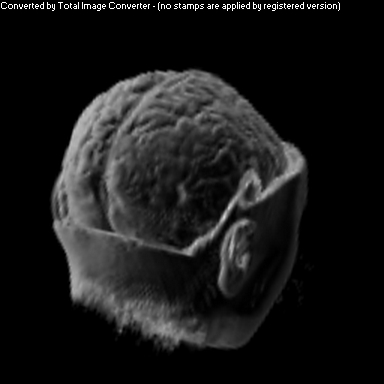
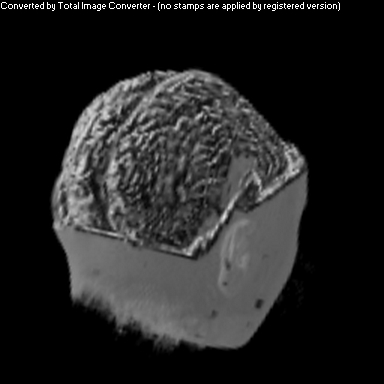
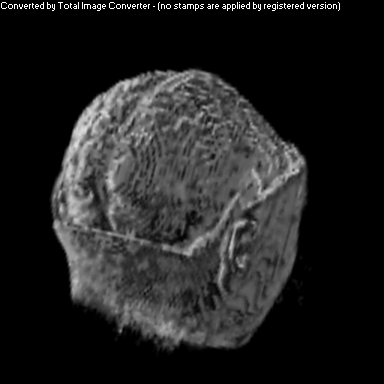
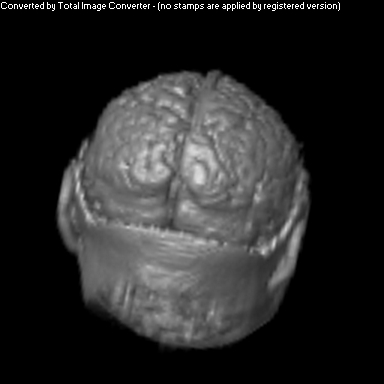
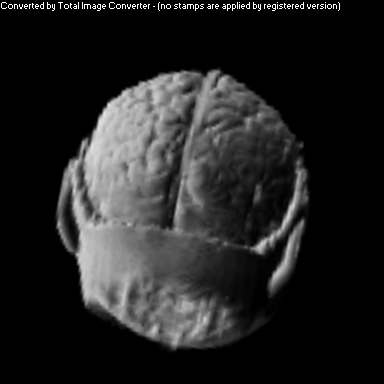
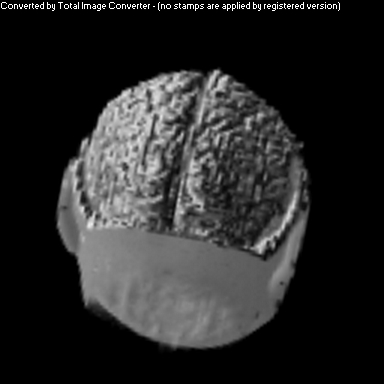
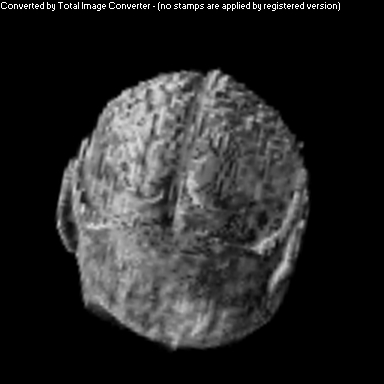
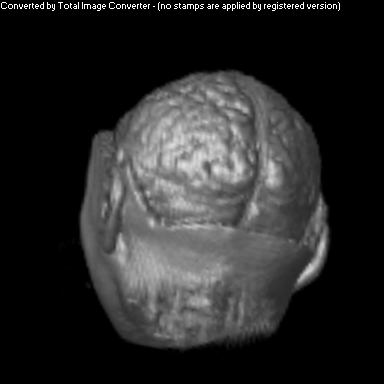

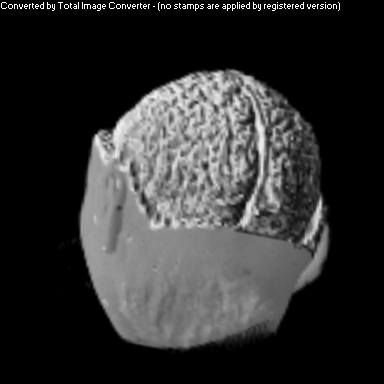

The purpose of this project was to implement a non-photorealistic shading algorithm for direct volume rendering. I used the Vol Pack volume rendering library, distributed by Stanford, as my base of code and implemented my own shader. The shading algorithm is based off of two ideas from non-photorealistic illustrations: toon shading and local lighting. The goal was to render a set of volumetric data in a way that gave high contrast to details and uniform lighting across the entire surface.
Toon shading replaces a gradual gradient from light to dark with discrete cutoffs between shaded and light areas. A popular example of this is cel shading in animation. This was achieved algorithmically by amplifying the color of each voxel, and then clamping that amplified color between -1 and 1. This effectively pushed almost all colors to one end of the spectrum or the other.
Local lighting replaces a discrete light source with light that is calculated per voxel across the volume. Before any rendering is done, a series of smoothed gradients is calculated for each surface voxel. A smooth gradient is calculated by taking the weighted average of a voxel's gradient along with the gradients of neighboring surface voxels. The weighting is a Gaussian function that is proportional to the neighbor's distance from the current voxel. These smoothed gradients are used to calculate local lighting at each voxel during the rendering stage. The light that intersects a voxel's gradient is the light vector that would be orthogonal to the next smoother gradient. This calculation is performed for every smoothed gradient of the voxel, and they are weighted and summed together to calculate the overall shading for that one voxel.
If you would like more detail regarding these algorithms, please see Rusinkiewicz's paper, linked at the bottom of this page. The paper originally describes this algorithm for a polygonal mesh. My project was to extend the algorithm for use with direct volume rendering.
Vol Pack's Shader |
Simple Cosine Shading |
Two Smoothing Passes (surface defined by density) |
Two Smoothing Passes (surface defined by gradient) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
As you can see above, I had mixed success with implementing the algorithm for the given volume. Part of this trouble came from my uncertainty about what defined the volume's surface. From above, it appears that density is a better indicator of surfaceness, although it washed out the skin on the face. I also had to do some guess work in translating the algorithm from polygonal meshes to direct volume rendering. As future work, I would like to spend more time investigating different ways of detecting surface in the volume and extending the weighting averaging to work better with voxels rather than vertices.