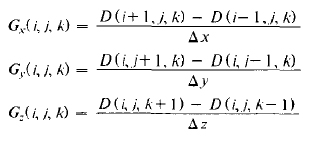Goal:
The initial goal for this project was to use a 4D volumetric dataset of a beating heart. Because of difficulties accessing the data, we used implicit functions to represent the same basic techniques that can be used when rendering time-varying volumetric data.
The goal of this project was to compute points along the surface of the implicit function and to render intermediate frames between the data timesteps by moving each point in timestep Tn through the gradient field of timestep Tn+1 until the points reach the surface defined in Tn+1. This approach is similar to Line Intergral Convolution (LIC) and the surface is generated using the method presented in "Marching Cubes: A high resolution 3D surface construction algorithm" by Lorensen and Cline with the assumption that at most one face passes through a voxel.
Algorithm:
- Generate values for time-varying implicit function
Values are generated by using an implicit equation with parameters (x, y, z, t) where a negative value is inside the surface and a positive value is outside the surface.
- Find location of surface
When the implicit surface intersects a voxel, the intersection points along the edges of the voxel are computed by linearly interpolating between the corners. When a single face intersects a voxel, there can be 3 to 6 points along the voxel edges that define the polygonal face. To find the value at the center of the polygonal face, we divided the face into triangles by iteratively splitting off triangles and analyzing the remaining polygon (See below). The center values for each triangle were calculated and the midpoint of all these centers used as an approximate value for the center for the whole polygon face.

- Calculate/assign gradient for all voxels
The gradient is computed for every voxel using the method outlined in Matching Cubes. The equations below are used to calculate the gradient where D(i, j, k) is the implicit function value at grid position (i, j, k) and delta x, delta y, and delta z are the dimensions of the voxel.
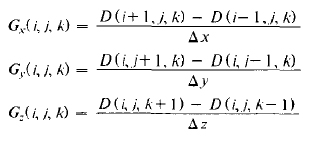
- Generate positions between time-steps by stepping along gradient
The position of points on the surface of Tn are updated by taking a fixed length step in the direction of the gradient associated with the voxel bounding the point in Tn+1. The position is updated for each frame until the surface defined in Tn+1 is reached by a specified fraction of the total points.
Results:
The program works very well. Volumes can be rendered with either points or splats and there is significant improvement in visual quality when generating intermediate steps for the Bump Sphere. Figures 1 through 3 demonstrate the different rendering options available using the implicit function of the sphere. Figure 4 shows the Bump Sphere and Figure 5 shows the "Flower".
Future Work:
- Implement Marching Cubes to render surfaces and deal with multiple faces intersecting a single voxel.
- Be able to specify the number of frames between time steps and how big the steps need to be to get to next surface
- Generate a new method for better determining the positioning of points on surfaces.
|

Fig 1: Rendering of Points with No Lighting

Fig: Rendering of Splats with No Lighting

Fig 3: Rendering of Splats with Lighting
|