The Kalman Filter Hole Filler
By Russell Palmiter
Project Description
The purpose of my project was to explore the use of a Kalman Filter as a way to predict the shape of missing geometry from an unstructured mesh. This process in general is referred to as hole filling, and to my knowledge this is the first attempt at using a Kalman Filter for that purpose.
Background Information
Hole Filling
Hole filling is a really important process in computer graphics because so many other modeling algorithms depend on the manifoldness of a mesh. And besides being a requirement for other algorithms, holes are generally visually displeasing (with exceptions of course) in a model, so being able to accurately fill a hole is a desirable ability.
Holes in a mesh can come from various places and are often
introduced as an undesirable side affect of another process. Two processes for
which the creation or holes is common are that of data acquisition and mesh
simplification. Data acquisition is frequently done by modeling tangible items using
tools like laser
rangefinders. This is done from several
vantage points, with the resulting range images integrated into a final model.
However, due to many factors including surface reflectance, occlusions, and
accessibility limitations, certain areas of the scenes are frequently not fully
sampled, leading to holes in the mesh.
Kalman Filter
The Kalman Filter is a technique for calculating the optimum estimates of process variables in the presence of noise. It works through a process of simultaneous recursion formulas that predict and correct estimates continually over the series of data points. The Kalman Filter is most frequently used to track a time-varying signal in the presence of noise, of which a natural application is digital signal processing. However, if you use the position of points in space as your variable (in the form of a series of discrete data points), and make a prediction for what your missing data points would likely be, it is possible to use a Kalman Filter to estimate what a series of missing geometry likely looked like (within some resemblance anyway).
Overview
Hole filling in general contains three major stages, which can
be identified as follows. Please not that these stages are my subjective qualification
for what I observed in other hole filling work.
Given
an unstructured mesh:
- Find Holes
Find the holes by keeping track of the
# of faces each edge is connected to, if you have a cycle of edges with only 1
face then those edges make up a hole.
A user defined threshold can be made
present if one wants to prevent certain holes from being filled. A good heuristic
for displeasure of hole is that of the number of edges in the whole. One could
also use geometric area of the hole, or cumulative edge length (perimeter).
Planarity of the hole is also another useful heuristic in determining which
holes the user may want filled, and which he or she may not.
- Triangulate the Hole
This is the process of taking the
polygonal hole and turning it into a set of triangles. creating
triangles
- Refine Triangulation
This is what my project focused on. This
step helps to refine the triangulation and make the geometry created more
accurate and visually appealing. More information can be found in the following
process section.
Process
To keep the problem as simple as possible while allowing me to explore more thoroughly the use of a Kalman Filter, I took many short cuts in the hole filling process. For example, I didn�t find the hole automatically; I simply had the user define a section of the mesh they wanted to be considered a hole. Then, as a best estimate for the missing area, I simply linearly interpolated between the edges of the missing geometry. I also used a limited number of uniformly distributes sample points.
The process in its entirety is really that of an application of a Kalman Filter, for which I will refer you to someone who can explain it better, Greg Walsh [see An Introduction to the Kalman Filter].
I�ve outlined the process graphically and presented it in both 2D and 3D below.
In 2D
I�ve done the process in 2D because it is usefully a demonstration and visualization tool.
Here is the original geometry (from what would otherwise be a mesh).
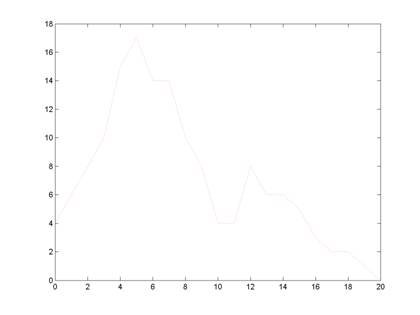
Original Geometry.
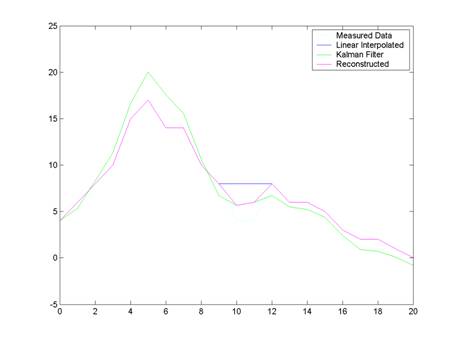
Here is the original geometry with a section of the graph missing data. The missing data has been linearly interpolated in place and this linearly interpolated data will later be used as an estimate for the Kalman Filter.
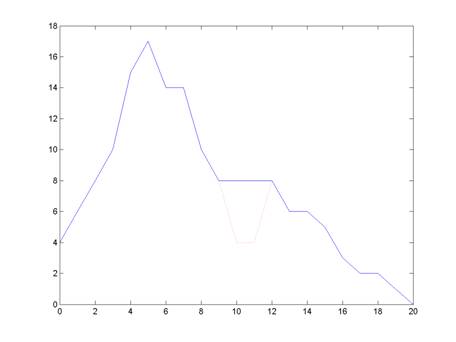
Missing Geometry aka Hole
(Note: Linear interpolation was used a an initial estimate for the area over the hole)
This next graph shows the Kalman Filter�s prediction for where the geometry should be. The section that corresponds to the hole will be put in place of the linear interpolation.
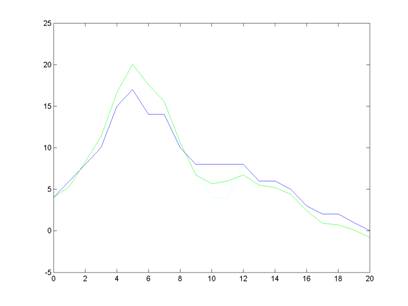
Kalman Filtered Geometry
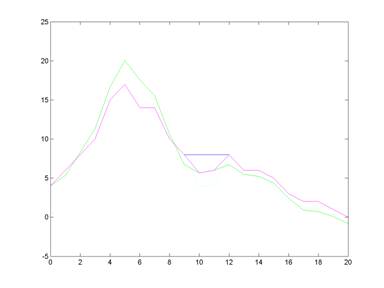
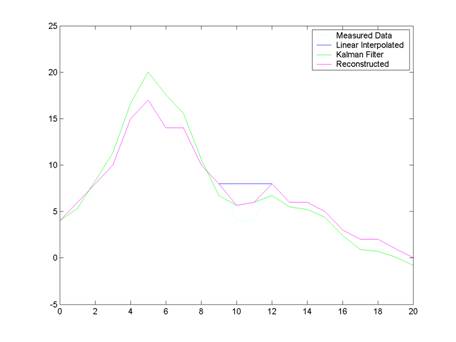
The magenta line is the reconstructed geometry using the kalman filter�s estimate in place of the missing data.
In 3D
Here is the same process again, except in 3D.
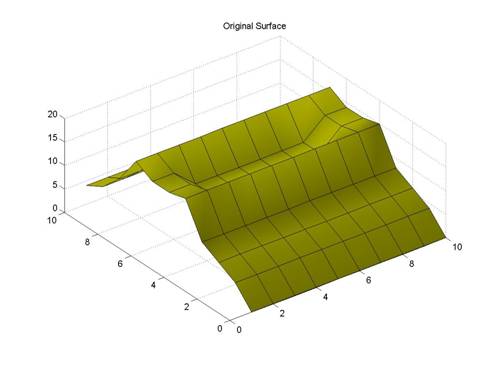
The Original Geometry
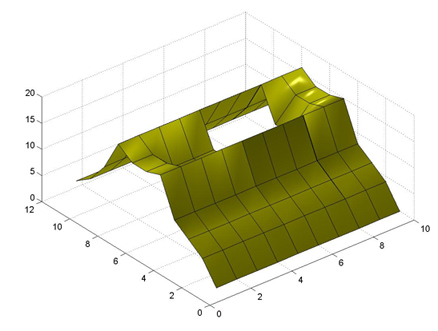
Geometry with a hole
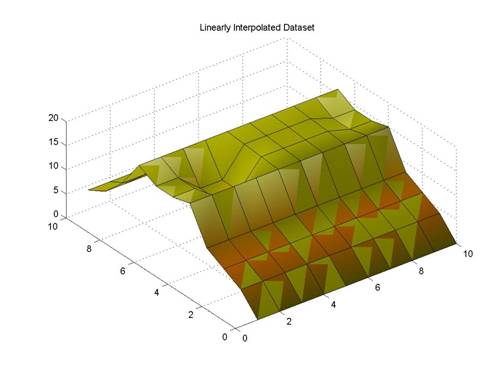
Geometry with the hole filled via linear interpolation
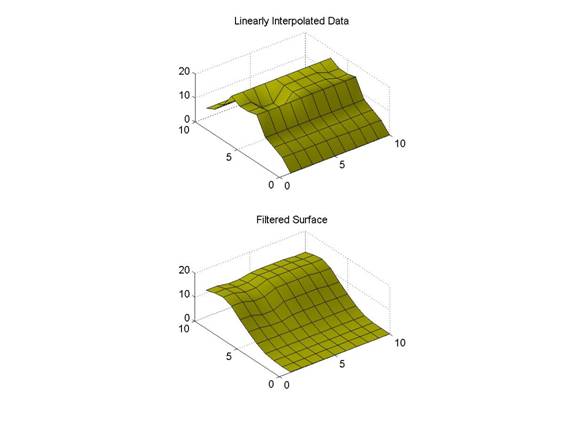
This comparison shows the linearly interpolated hole (this is the geometry that�s fed into the filter) vs the Kalman Filtered geometry. Notice the smoothing effect which makes this method also serve as a good geometry smoother.
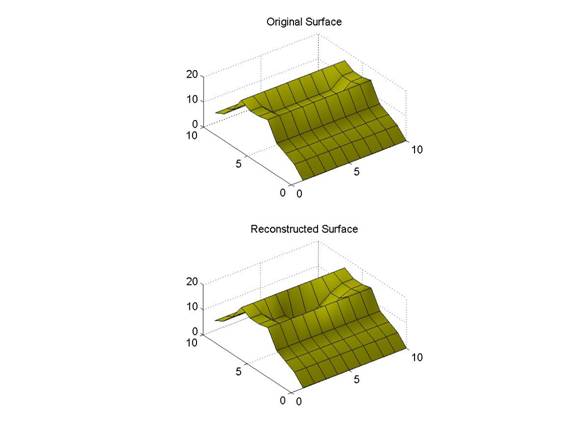
Here is the results of the 3D Kalman Filter. Notice the dip in the geometry that wasn�t present in the linearly interpolated fill for the hole. The dip is certainly not perfectly aligned with the original, but it is present which means the Kalman Filter must be doing an alright job.
Presentation
My presentation was short and sweet and focused around me speaking to the demo, but in the case that you missed something on one of my slides or weren�t able to attend my demo; I have included the slides here for your viewing pleasure.
Results
The results for this project have not been measured in a formal way, although I think you will agree that they do show visually appealing results. In completing this project, I have found that the Kalman Filter can not only be used for hole filling, but would also make a very nice geometric smoother.
Final Thoughts
This project was a great learning experience for me and I�m
glad I chose it. I don�t know that I came up with the best hole
filler. I think I came up with what looks to be a pretty good geometry smoother
more than anything. I think I did prove that it�s possible to fill geometry
using this method, and I think that�s quite an accomplishment. In fact, I think
applying a Kalman Filter at all is quite an
accomplishment. I�m pleased to see that it did an okay job too. I would love a
metric to allow me to measure how well I predicted the geometry and the ability
to compare it to other methods (like simple linear interpolation). Then I would
run that on several different methods with randomly generated and lost geometry
and report percentages of improvement.
Future Work
Fully implement the hole filling process, from discovering the hole, to triangulating over the hole, to then refining the triangulation.
Use a better estimate for the initial for the missing geometry. Perhaps a more current hole filling method. This would help my Kalman Filter considerable, and with their power combined, there would be no stopping them.
Use the Kalman Filter to predict/fill other attributes as well. This should be a relatively simple task for the Kalman Filter, but might require adaptations. Example attributes one might like to predict for the hole are texture data and normal data (as well as many others).
Use a heuristic to measure how close the reconstructed geometry is to the original. This could then be used a measure of quality for the hole filler and adjustments and tweaks could be made to the parameters of the Kalman Filter. A good heuristic to use would be the quadric geometric error metric (quadric error metric or qem).
Implement the project in C++.
References
Hole Filling
http://www.cs.utah.edu/research/techreports/2004/pdf/UUCS-04-019.pdf
http://www.cs.sunysb.edu/~jianning/Jianning_Files/Sib03.pdf
http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=1240986
http://www.geom.uiuc.edu/docs/forum/hoops_links/khoops.html
Kalman Filter
http://www.cs.unc.edu/~welch/kalman/
http://en.wikipedia.org/wiki/Kalman_filter
Matlab
http://www.mathworks.com/academia/student_center/tutorials/launchpad.html
http://www.glue.umd.edu/~nsw/ench250/primer.htm#sec14
http://www.math.utah.edu/lab/ms/matlab/matlab.html
http://www.mit.edu/people/abbe/matlab/main.html
[A word document of the material covered by this webpage can be found here]