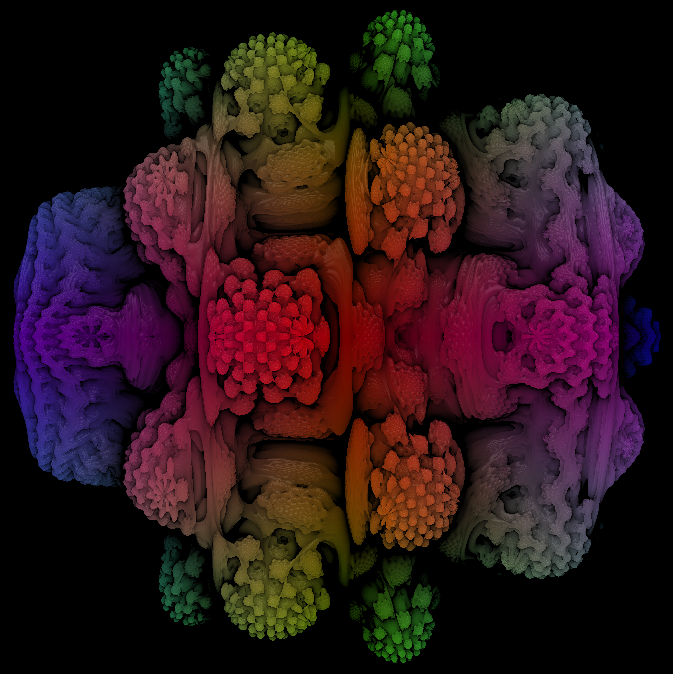
This quarter we developed CUDA powered raytracers. I used mine to visualize a math equation called the Mandelbrot Set. When represented in 3D coordinates, each point is a hypercomplex number that is either inside or outside the set. The points in the set create a surface that is an interesting fractal pattern.
Rendering The Mandelbulb
Fig1, Final render, each frame took approx 1.1 seconds to raytrace on a Quadro 1000M (laptop graphics card).
Raytracing
For each pixel, a ray is cast from the camera position towards the mandelbulb. The intersection of the ray and the mandelbulb will be the surface of the final render.Marching Rays
In order to find this intersection, small steps are taken along the ray. At each step the distance from the surface is estimated and then the ray marches that distance forward. With a good enough distance estimation, the intersection of the ray and surface will be found.
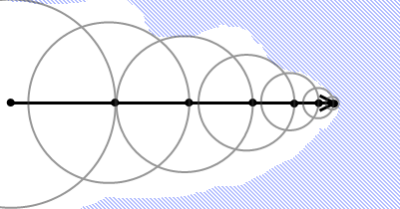
Fig 2, example ray marches toward the surface (image from this blog)
Distance Estimation
The heart of the algorithm is the distance estimation function. The input is a 3D vector (which represents a complex number), and the output is a guess to how far the surface is. The distance estimation function I implemented is the scaler distance estimator from Mikael Hvidtfeldt Christensen's blog post on fractals.
Shading
Shadows are only approximated. The more marches a ray takes, the more occluded the surface is at the point, so less ambient lighting is applied. This means areas closer to the center are darker.
The distance estimation function can also be used to approximate a normal, by checking how the function changes in all three coordinate directions. My render includes a point light that provides direct and specular lighting based on this normal.