Probabilistic Models Based on Shape

Components for Random Tree Generation

Ryan Staab

CSC 570 – Dr Wood

3-21-2013

Overview:

Based on the work http://people.cs.umass.edu/~kalo/papers/ShapeSynthesis/.

I generate randomly shaped trees by combining different styles and numbers of three basic components: trunk, branch, and leaf.

The styles and number of each component are sampled from distributions of random variables defined by a Bayesian Network.

Bayesian networks:

-Directed, acyclic graph with each node representing a random variable (either continuous or discrete).

Parent node random variables influence the distribution of child node random variables, or more formally, child nodes have conditional probabilities dependent on parent nodes.

The model:

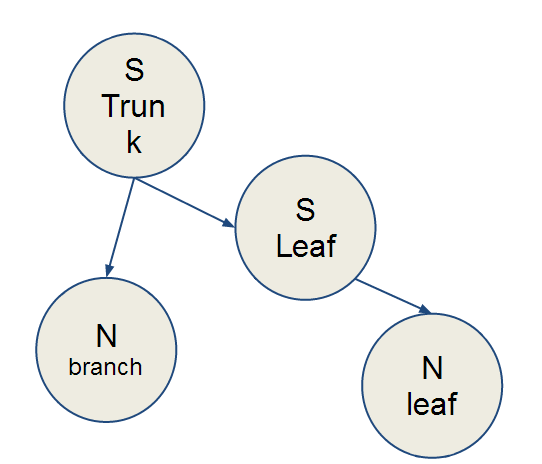
-Two kinds of trunks (thick, thin)

-Two kinds of leaves (pointy, bushy)

-Variable number of branches (2-5). Thick trunk trees can only have 2-4 branches.

-Variable number of leaves per branch (1-2). Bushy leaves cannot appear in pairs.

-Additionally, tree height and tree orientation (rotation) have been randomized independent of the model.

We can tabulate the conditional probabilities represented in the model, and compute the marginal probabilities for each random variable by summing the rows or columns.

Shown here is the conditions between Trunk and Leaf styles.

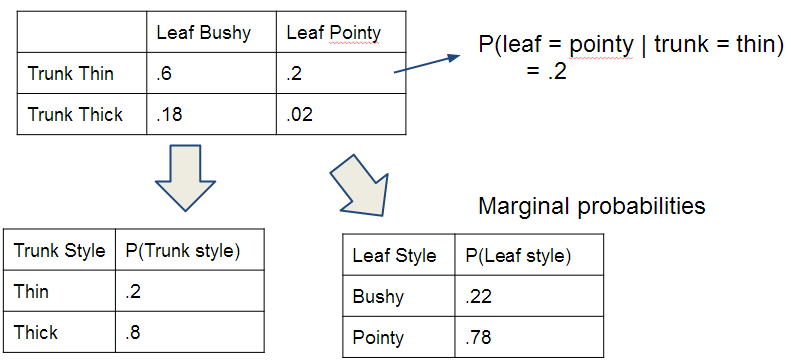
Common trees:

Tree with two leaves per branch:

Rarer trees:

Implementation details:

Each random variable has its own associated STL vector.

When I sample the random variables, I simply push a new value into each random variable vector for each tree that I will output onto the screen.

Conditional probabilities are implemented with cascading if-else statements based on ranges from rand() % 100

and the values of parent variables (the vectors for parent variables are filled first).