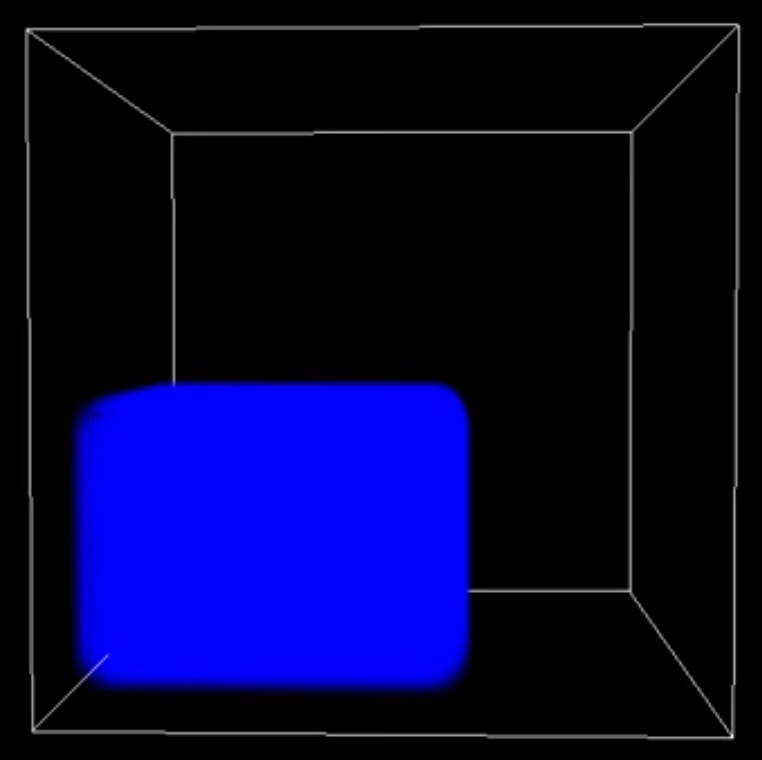
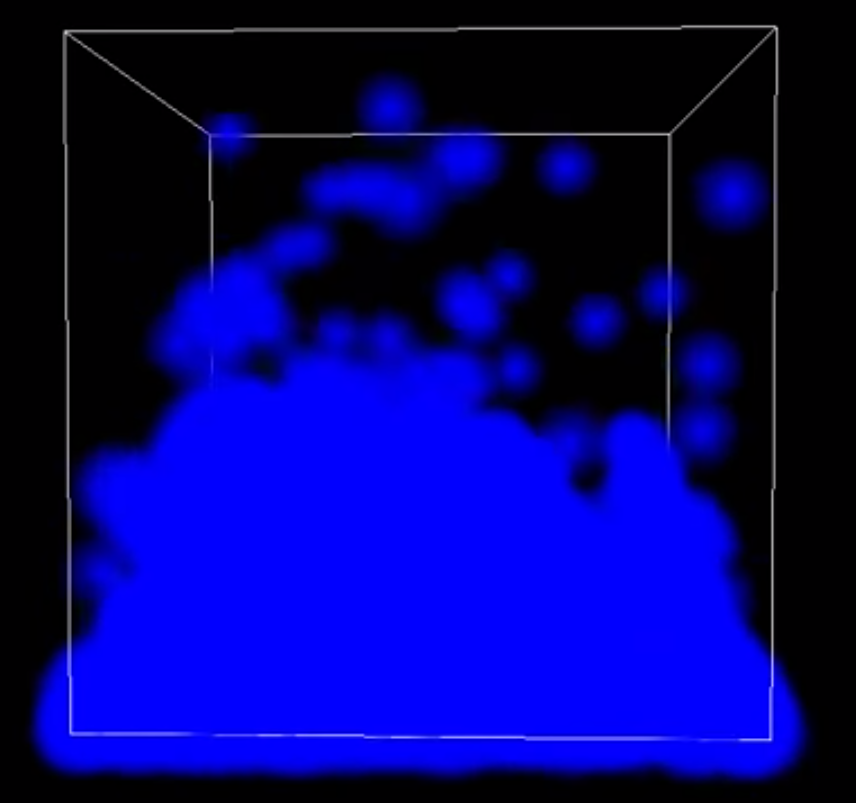
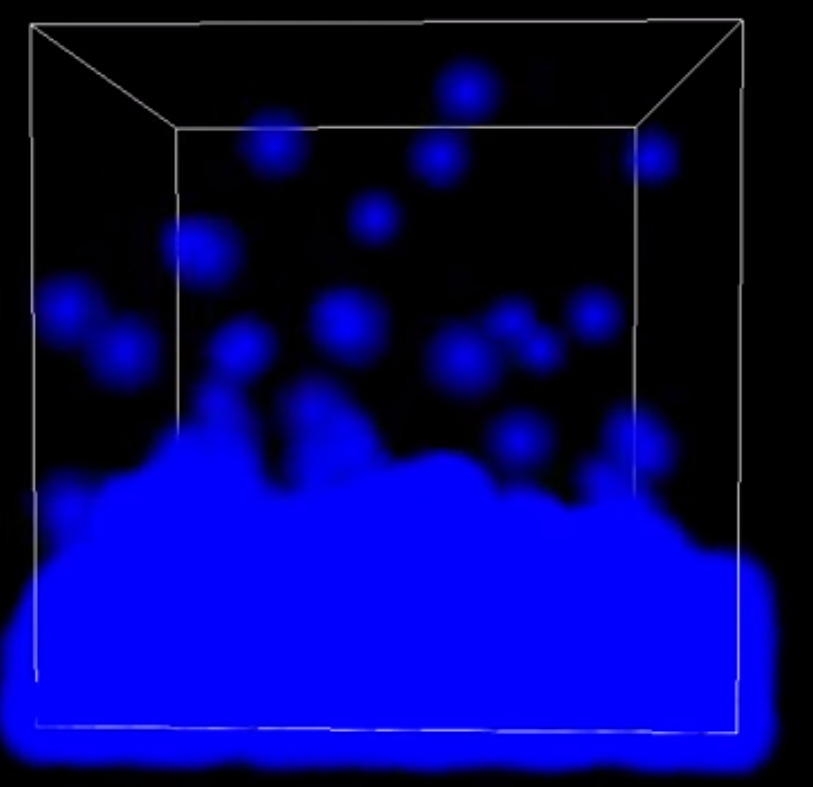
Fluid Simulation
Main Equation
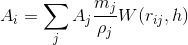
A scalar quantity can be determined for each particle by weighing that quantity from nearby particles with an appropriate kernel function.
Density
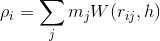
rho (density) can be calculated with the mass of the particle and the default kernel function.
Navier-Stokes Equation
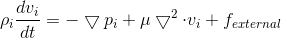
Updating a particle's position and velocity will be based on this equation for fluids. Pressure gradient, viscosity, and external forces (gravity) are required to solve this equation.
Constants
From Lagrangian Fluid Dynamics Using Smoothed Particle Hydrodynamics
- Mass = 0.2
- Stiffness = 3.5
- Ideal Density = 1000
- Viscosity = 3.5
- Support Radius (h for Spatial Hashing) = 0.0625
- Smoothing (h for kernels) = 0.0625
Navier-Stokes Equation Breakdown
Pressure Gradient
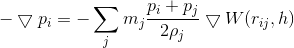
Pressure Gradient is how much the particle is affected by other particles.
Viscosity
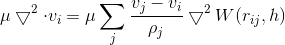
Viscosity is how much particles will stick together.
Gravitational Force
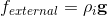
External forces: gravity
Kernel Functions
Default
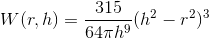
Kernel Function to calculate density. h is the smoothing constant used to calculate which particles to use to affect the current particle.
Pressure
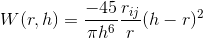
Kernel Function for calculating pressure gradient
Viscosity
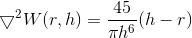
Kernel Function for calcuating viscosity
SPH
SPH with Spacial Hashing
Implementation
Code Algorithm to Update Particles with SPH
Algorithm obtained from Efficient Neighbor Search for Particle-based Fluids paper. Describes how to calculate SPH with Navier-Stokes and Kernel Functions.

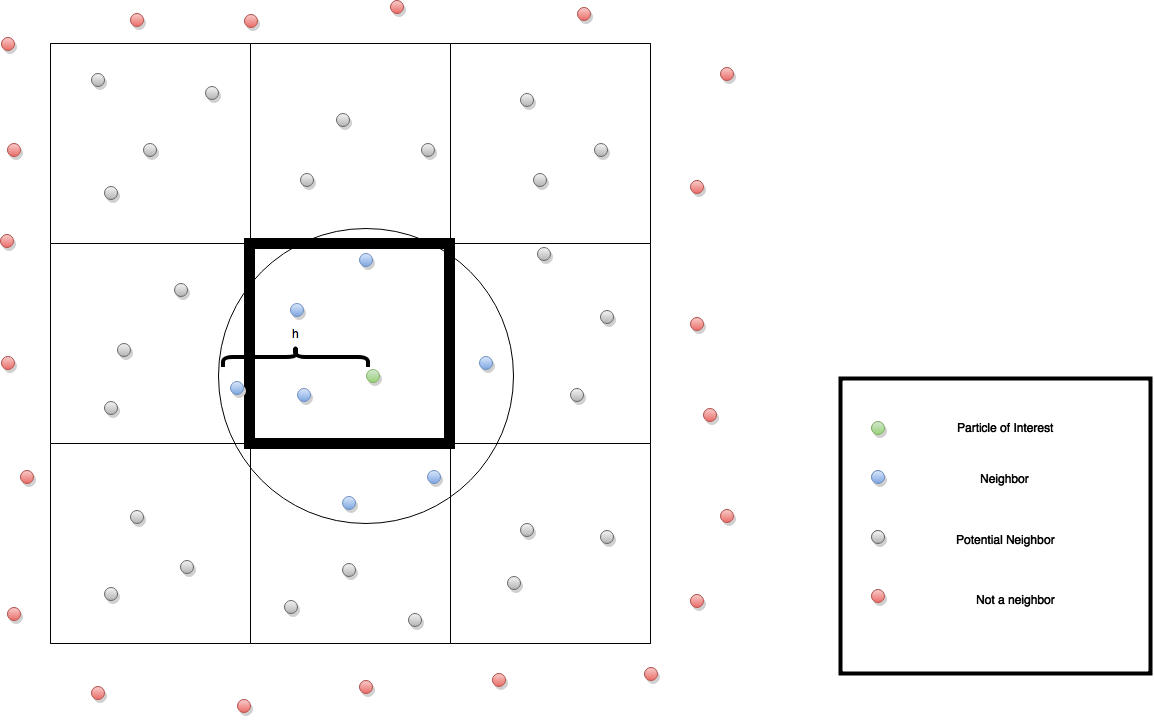
Spatial Hashing
The naive way of implementing SPH would be to check all particles with each other to see if they interact with each other. This makes runtime O(n2). To speed up the runtime, we can run an algorithm called the nearest neighbour algorithm that will only have particles interact with each other if they are close enough. Particles are "close enough" to each other if they are within the radius of support distance (h). Runtime will be reduced to be O(nm), where m is the average number of neighbours. The diagram to the left is an example of it in 2D. Each cell is given a number and each particle is given the location it is in. Then to detect neighbors, it grabs the nearby cells. My project does this in 3D, where instead of 9 cells to look it, it becomes 27.