CSC 572, Spring 2016

Project Description
The goal of this project was to impelment a basic Dual Contour isosurface extraction. The extraction should try and match the extraction proposed in Dual Contouring of Hermite Data, and should utilize both the zero crossing, and the normal data of a volume.Video
Algorithm Details
Octree

The data structure used to store the Hermite data is an Octree. Each leaf of the octree is tagged with it's value in the underlying volume strucutre. The tree is maximally collapsed, meaning every leaf in the tree will cross the isosurface. I used a fairly basic Octree as a base, and built additional functionality into it as I continued working with the project.
QR Representation of a Quadratic Error Function
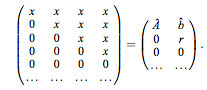
Minimizing the QEF was the hardest part of the project. I was able to do so, with insights gained from reading the follow up paper, Dual Contouring, The Secret Sauce. This paper discussess the algorithms presented in "Dual Contouring of Hermite Data" in more detail, including information on the breifly mentioned centroid of intersection points. (Dual conturing of Hermite Data, Page 4). With this information, I formulated the following algorithm:
For every leaf in the maximally collapsed octree
- Create a 4x4 Zero matrix as the basis of the QR decomposition.
- For every intersection point in the leaf
- Find one intersection point pi with normal ni
- Append the vector [ ni.x, ni.y, ni.z, dot(pi,ni) ] to the bottom of the 4x4 matrix
- Use a series of Givens rotations to trianglulate the matrix.
- With this newly formed matrix, Extract A', and B'
- Compute the SVD Decomposition of A'TA', and use it to solve the linear equation A'TA x = (A'T B' - A'TA' c) , where c is the average of all intersection points on the mesh. I found Eigen::JacobiSVD useful for this step.
- Compute the vertex position, v by adding c and x
- If the vertex position falls outside of the leaf, set the vertex position to the centroid.
- Calculate the normal at the new vertex position.
Building the Mesh

Computing the final mesh requries many lookup tables, and a few clever recursive functions. My main focus was on positioning the vertex, so I used a reference to build my final triangle mesh. The refrence I used can be found at https://github.com/nickgildea/DualContouringSample in the Octree.cpp class.
Results
I was able to successfuly create a mesh from both volume data, and implicit equations. My mesh exhibited several aspects of Dual Conturing, including the sharp edges outlined in the initial reading. I was able to use the paper's proposed QR-like storage of the QEF to do all of my calculations with floating point precision. My results are not exact, and there is currenlty no simplification of the octree. There are still a few issues regarding the shading of complex models, but a solution is proposed in the reference linked above.
Glitches


Sources
"Dual Conturing of Hermite Data" http://www.frankpetterson.com/publications/dualcontour/dualcontour.pdf
"Dual Contouring, The Secret Sauce": http://www.cs.berkeley.edu/~jrs/meshpapers/SchaeferWarren2.pdfl
Dual Contouring Sample Source Code. hhttps://github.com/nickgildea/DualContouringSample