Overview of Project
My final project for the class was to investigate and implement a GPU mesh voxelization algorithm, similar to that used in voxel cone tracing for indirect lighting (see more here), following an overview provided by Patrick Cozzi and Christophe Riccio in their chapter in OpenGL Insights (see here). The goal of the project was to try and implement the GPU voxelization algorithm so that any arbitrary triangle mesh could be voxelization every frame at a real-time framerate. My primary motivation for wanting to do so was to continue investigating making things render fast and potentially doing more with voxel cone tracing in the future (for which this is a necessary pre-requisite). Also, I knew this would make me do "non-traditional" things with the GPU for it to work, which is a weaker area of mine that I wanted to improve.
How to Voxelize the Mesh
Voxelizing a mesh on the GPU requires us to use what the GPU is good at - doing the same operation on a lot of data. However, our goal is to check whether or not a particular part of a triangle falls within a voxel (and which voxel). To do so, we first transform our input triangles into orthographically projected triangles along their dominant normal axis (see below). This ensures that the largest possible triangle surface is provided to check if the 2D projection of a triangle intersects the 2D projection of a voxel.
Triangle Projection Method
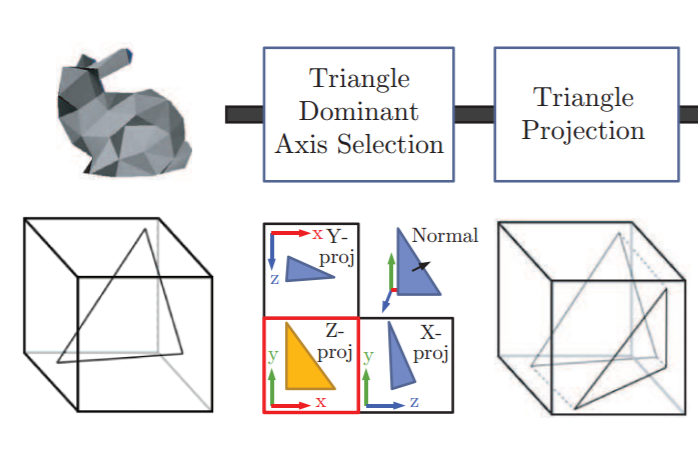
Now that we have these newly projected triangles, we can compute our lighting information as usual (I used a simple Phong shading model) and place our triangle fragment into the correct voxel.
Implementation Details
The pipeline for GPU voxelization starts with the usual pushing of mesh data to the GPU and a relatively standard vertex shader, with the notable exception of only wanting to transform the vertices into world space using the model transform. Then we need to figure out how we are going to project our mesh based on each triangle's normal dominant axis. Luckily, the geometry shader is here to save us and provides the perfect method to have a view of an entire triangle. This makes it simple to get the triangle's normal and choose the view matrix for the dominant axis to orthogonally project the triangle (multiplied by an orthogonal projection matrix as well of course).
Pipeline Description
The geometry shader than outputs brand new, orthogonally projected vertices perfect for our needs. The fragment shader then colors the fragments and uses its interpolated position to index into the voxel map (a 3D texture). This data can then be used to render a visualization of the voxel grid using cubes or a wireframe, or used in places like voxel cone tracing as previously mentioned.
Results
My project results were promising but less than ideal. I was able to successfully project the mesh and get a correct shading of the mesh for voxelization (see below), but I was unable to verify a complete voxelization using a true visualization of the voxel grid or similar.
Bunny Mesh With the Orthogonally Projected Version (parts projected in the x-axis, y-axis, and z-axis)
The Orthogonal Projections Separated Out
What I Learned
While my overall project result was not as successful as I had hoped, I learned a ton from the process. A lot of what I learned was in some of the more advanced OpenGL techniques that I hadn't had a chance to use like the geometry shader and 3D textures. I also learned some effective GPU debugging techniques and really understand the importance of having good debugging techniques at the ready for this kind of GPU work. In addition, I obviously also learned a lot more about voxelization and gained a solid understanding of voxel cone tracing in the process.