Transvoxel

Overview

For my final project in CSC 572 (Grad Computer Graphics), I chose to implement the Transvoxel Algorithm.

"The Transvoxel Algorithm is a method for seamlessly stitching together neighboring triangle meshes generated from voxel data at differing resolutions so that level of detail (LOD) can be used with large voxel-based datasets such as volumetric terrain in next-generation video games." - Eric Lengyel

This algorithm was invented by Eric Lengyel back in 2009 and published in 2010. For my implementation, I wanted to procedurally generate voxelized terrain with various levels of detail (LOD) that was fully destructible in real-time.

This screenshot is taken from Eric Lengyel's C4 Engine and shows a large voxel-based terrain having three levels of detail rendered in real-time with several thousand trees and multiresolution cascaded shadow maps.

But before I dive into the implementation, let's look at some background...

Procedural Generation

Procedural generation is the process of a computer generating content rather than a human artist or designer. This alleviates much of the time and money spent on hiring human artists and has the potential to quickly create a vast amount of interesting content. For this assignment, I wanted to procedurally generate terrain. To do this, I used an algorithm called Simplex Noise. You may have heard of its predecessor, Perlin Noise. Both were created by the same man, Ken Perlin, but Simplex Noise is known to be faster, have fewer artifacts, and work at higher dimensions.

To generate terrain using Simplex Noise, either 2D or 3D Noise can be used...

2D Noise

To generate terrain using 2D Simplex Noise, people use what's called a 2D heightmap. This is basically a grayscale image where the pixel intensities correspond to the heights of the terrain vertices. If you have a 256x256 image, then your terrain will have 256x256 vertices and will be a perfect square. The 2D heightmap is generated using Simplex Noise by sampling the noise function at each pixel location (x, y) and storing the result in the heightmap. Using just the values from the noise algorithm may give seemingly random noise, but following a process called Fractal Noise can give very realistic heightmaps.

Simplex Noise

Fractal Perlin Noise

One of the limitations of using 2D heightmaps is that no overhangs, vertical cliffs, or caves can be created, which limits the realism that can be achieved. This is fixed if we use 3D Simplex Noise.

3D Noise

To generate terrain using 3D Simplex Noise, the same process is followed as for the 2D noise, except we use a 3D grid of values (x, y, z). However, now the values can't correspond to the height of terrain vertices. Instead, each value corresponds to an isovalue of the 3D terrain surface. An isovalue is 0 if it lies exactly on the surface, negative if it is within the terrain, and positive if it is outside of the terrain. A simple example is a sphere. The isovalues in a 3D volume correspond to the distance from the surface of the sphere, with 0 being on the surface, negative values being within the sphere, and positive values being outside of the sphere.

3D Noise

3D Noise w/ Voxel Cubes

To generate triangles from a volume of isovalues, several methods exist: Marching Cubes, Surface Nets, Dual Contouring, and maybe others. For this implementation, I used Marching Cubes. A good tutorial page with code examples can be found here.

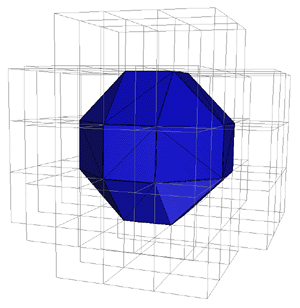
Marching Cubes

And now we have voxelized terrain! YAY! :D

This is where Transvoxel comes in...

Transvoxel Algorithm

The Transvoxel Algorithm can be split into several steps:

Modified Marching Cubes
Level of Detail (LOD)
Transvoxels
Shading / Texturing

Modified Marching Cubes (Ch 3)

The first step was to implement a modified version of Marching Cubes that fixed some inconsistencies with the original tables that could create holes in the terrain in certain situations. Eric Lengyel provides the modified tables here. It was pretty straightforward to implement this. Pretty much just implement Marching Cubes, but use these tables instead.

High Performance Implementation

Eric Lengyel also went over a high performance implementation that focused on reusing as many vertices as possible and sectioning the terrain into 16x16x16 blocks. I don't think it would be too difficult to implement this part, but I ran out of time and skipped it as it was not necessary for my simple implementation.

Level of Detail (LOD) (Ch 4)

The second step was to use LOD to simplify the terrain geometry and reduce the number of triangles being rendered based on distance from the viewer. Each LOD reduced the resolution of the volume by a factor of 2 in each dimension. This was required in order for the Transvoxel Algorithm to work properly. In general, the highest resolution LOD would be used within the closest proximity to the viewer. The farther away you go, the lower resolution the LOD would be. Each block of 16x16x16 voxels would be a single LOD. When changing the LOD, the block would resize to contain 16x16x16 voxels at the new resolution.

LODs

In my implementation, to showcase the LOD, I just decreased the resolution of the LOD halfway along the Z axis. This allowed me to not worry about using blocks of voxels and to not worry about varying the LOD relative to the viewer's location.

LOD 0 Hole

LOD 1 Hole

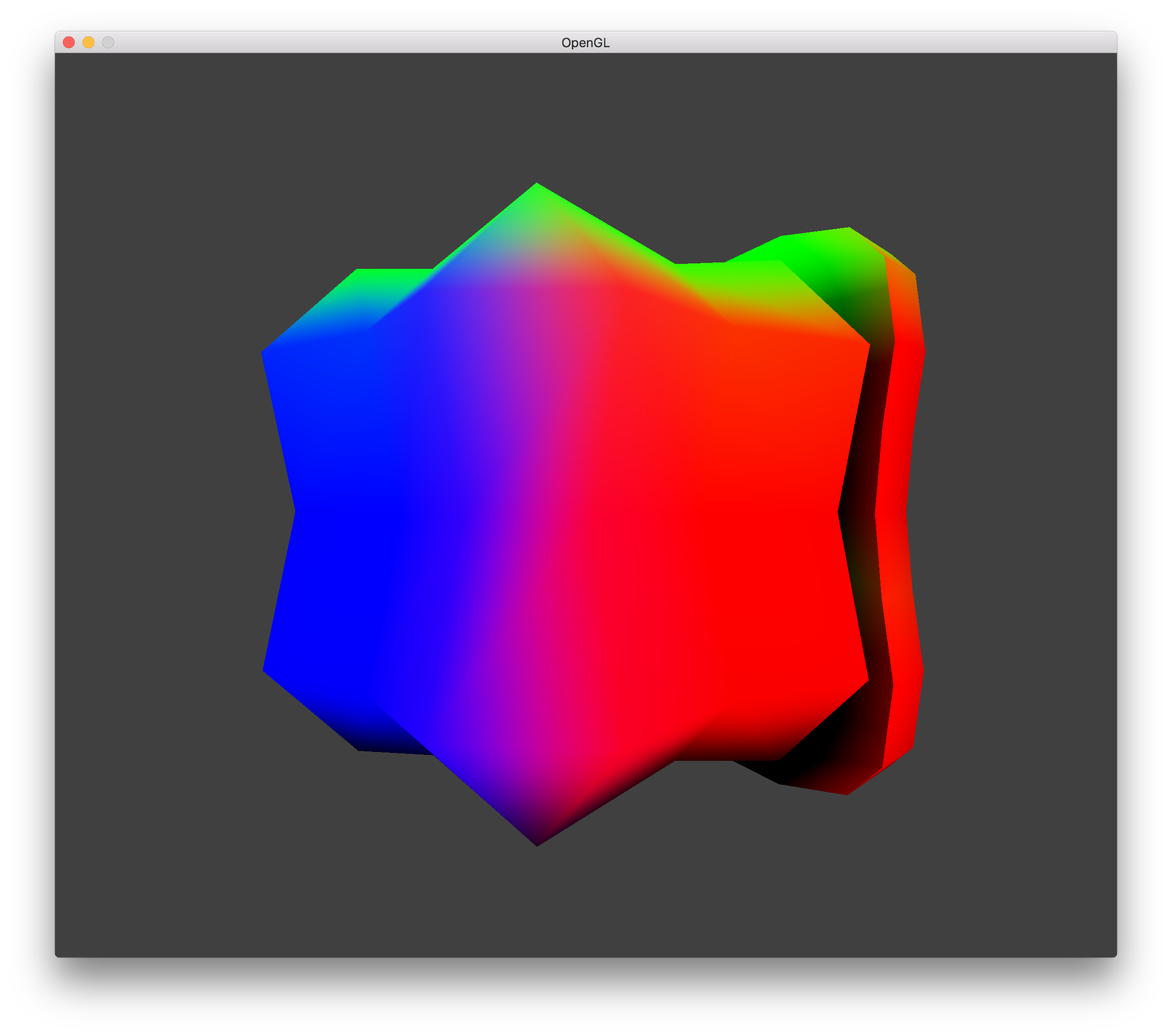
LOD 2 Hole

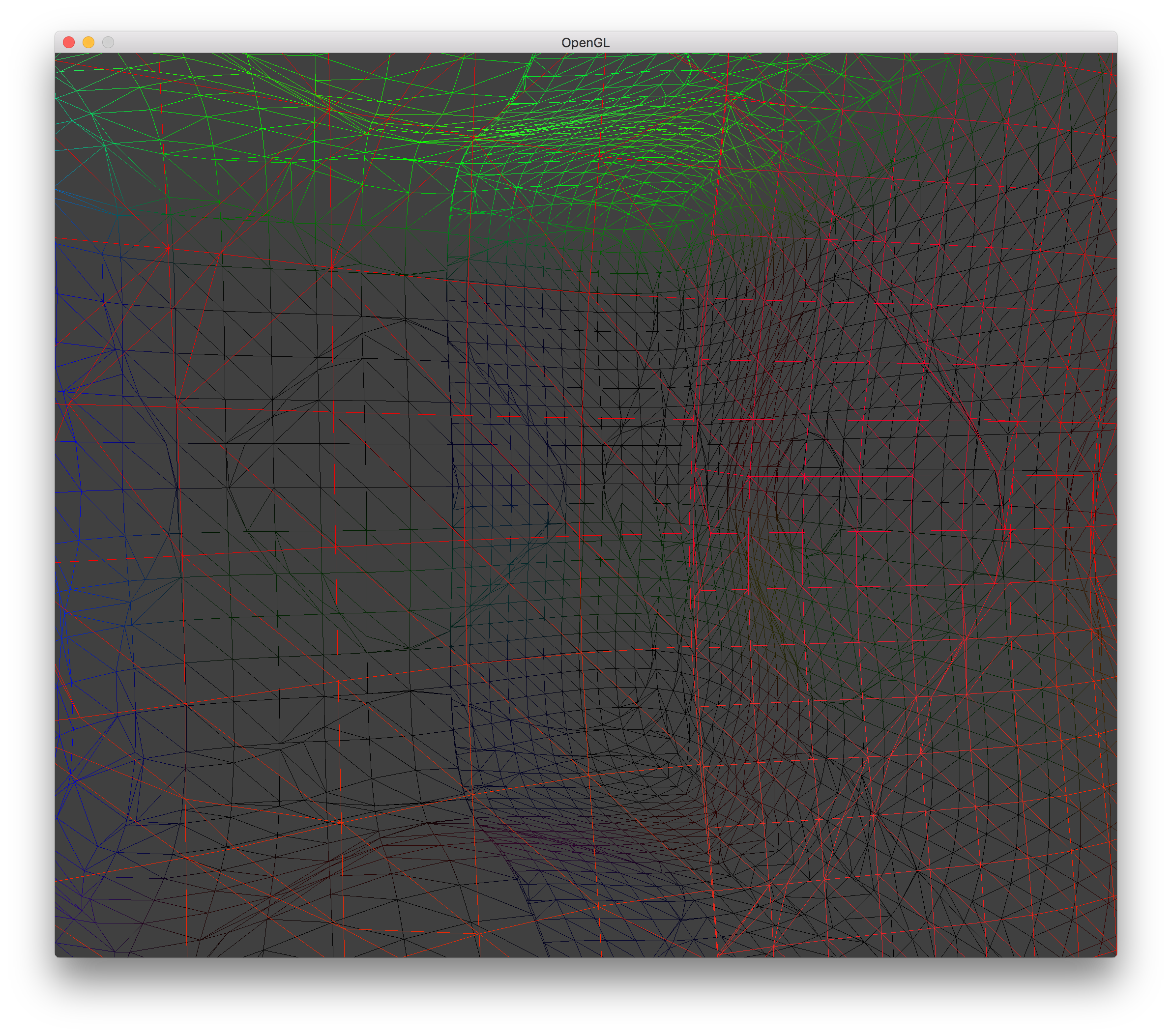
LOD 0 Hole Wireframe

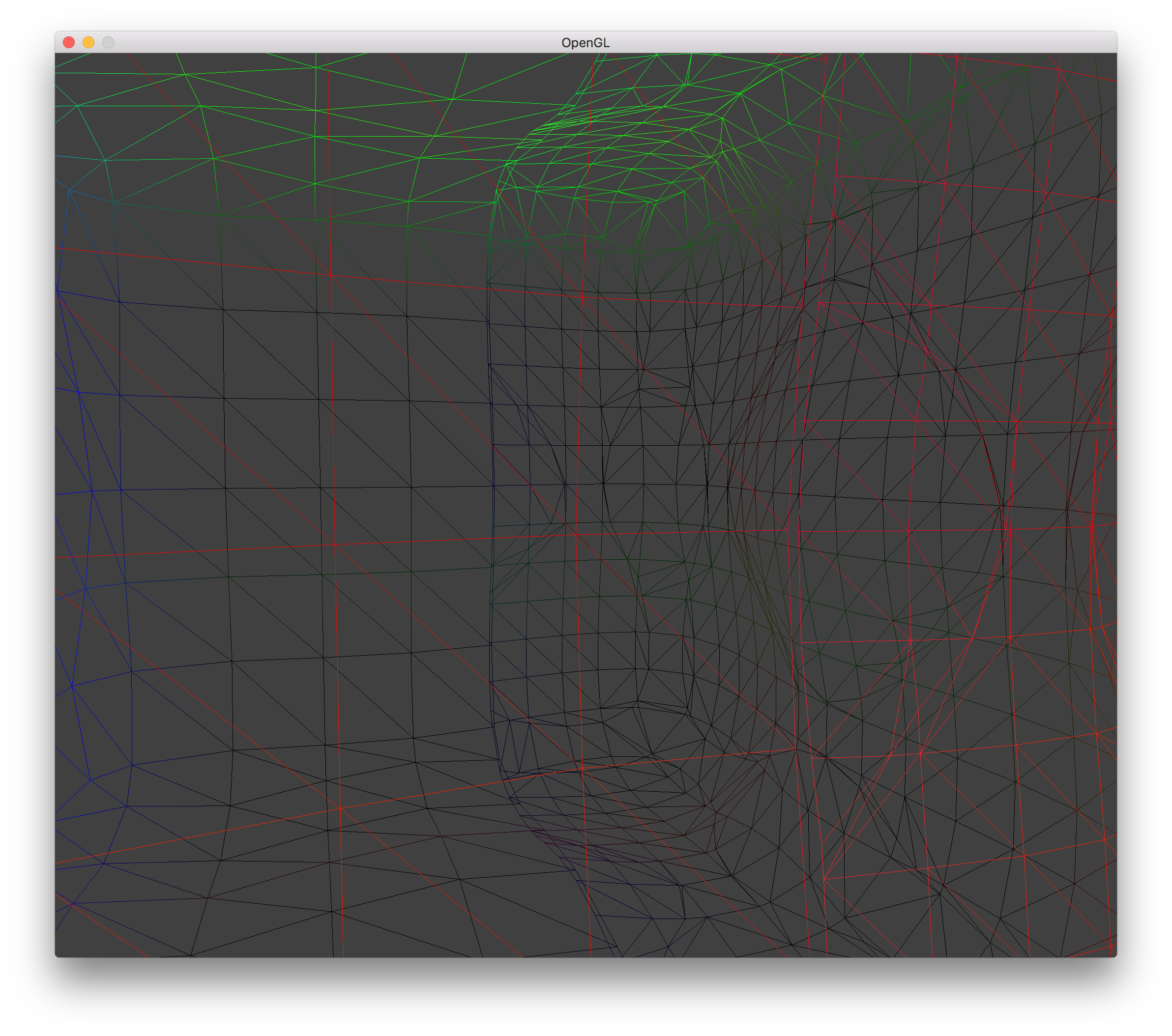
LOD 1 Hole Wireframe

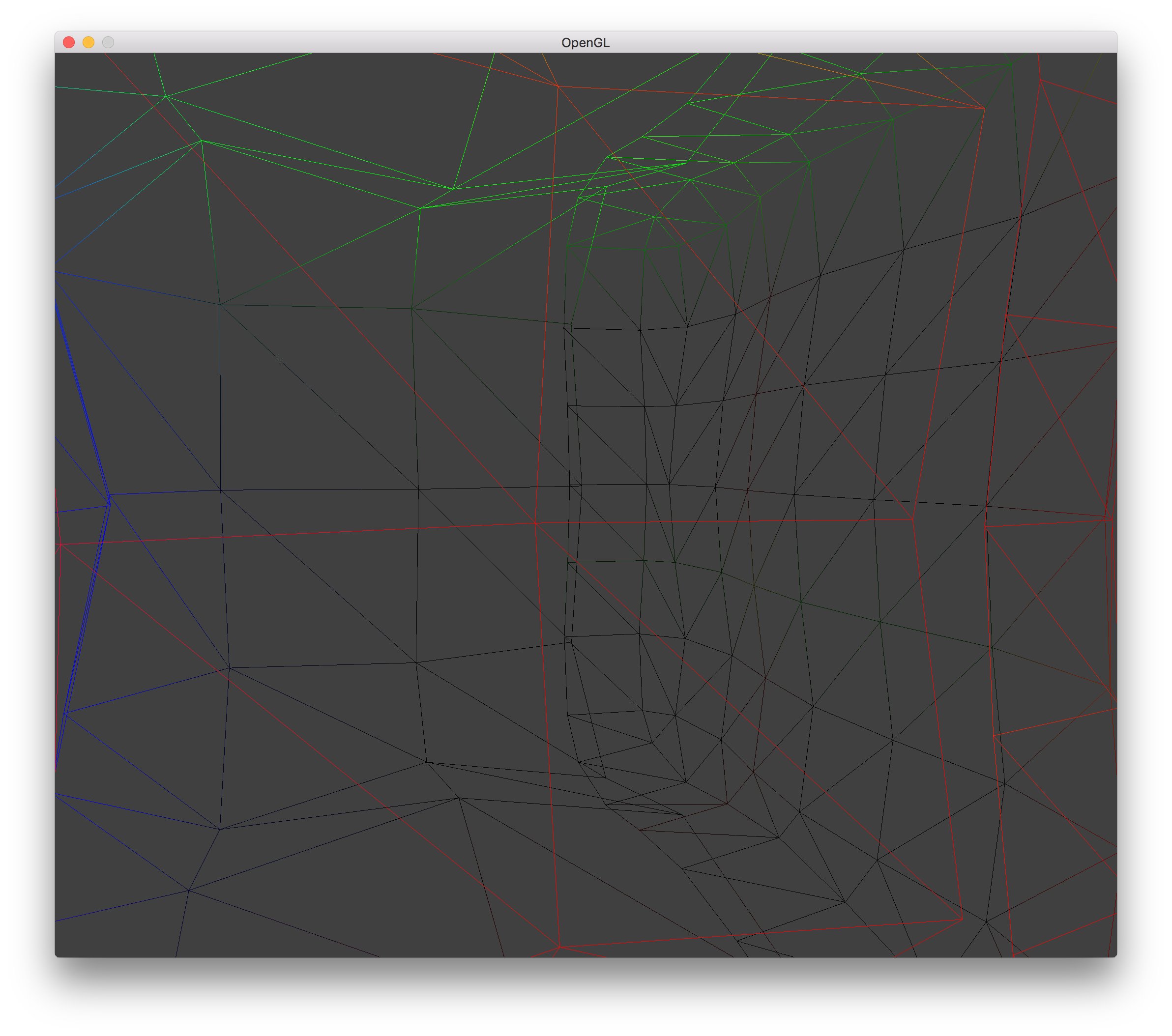
LOD 2 Hole Wireframe

Surface Shifting

When rendering the terrain for 2 LODs, the transition between the two LODs will usually have a hole. This is due to the sampling of the isovalues for a voxel only occurring at the corners and generating the triangle vertices based upon these values. IMAGE. The triangle vertices will vary depending on the LOD used. To remedy this problem, when calculating the triangle vertex position along an edge of a lower resolution LOD, we recurse on that edge to sample the isovalues at higher resolutions in order to precisely choose the triangle vertex location. This fixes the issue where changing LOD can cause the terrain to shift up or down, which can physically move objects that were sitting on the terrain and look bad from a viewer perspective. With this fix, even at lower resolution LODs, the terrain should not shift its position.

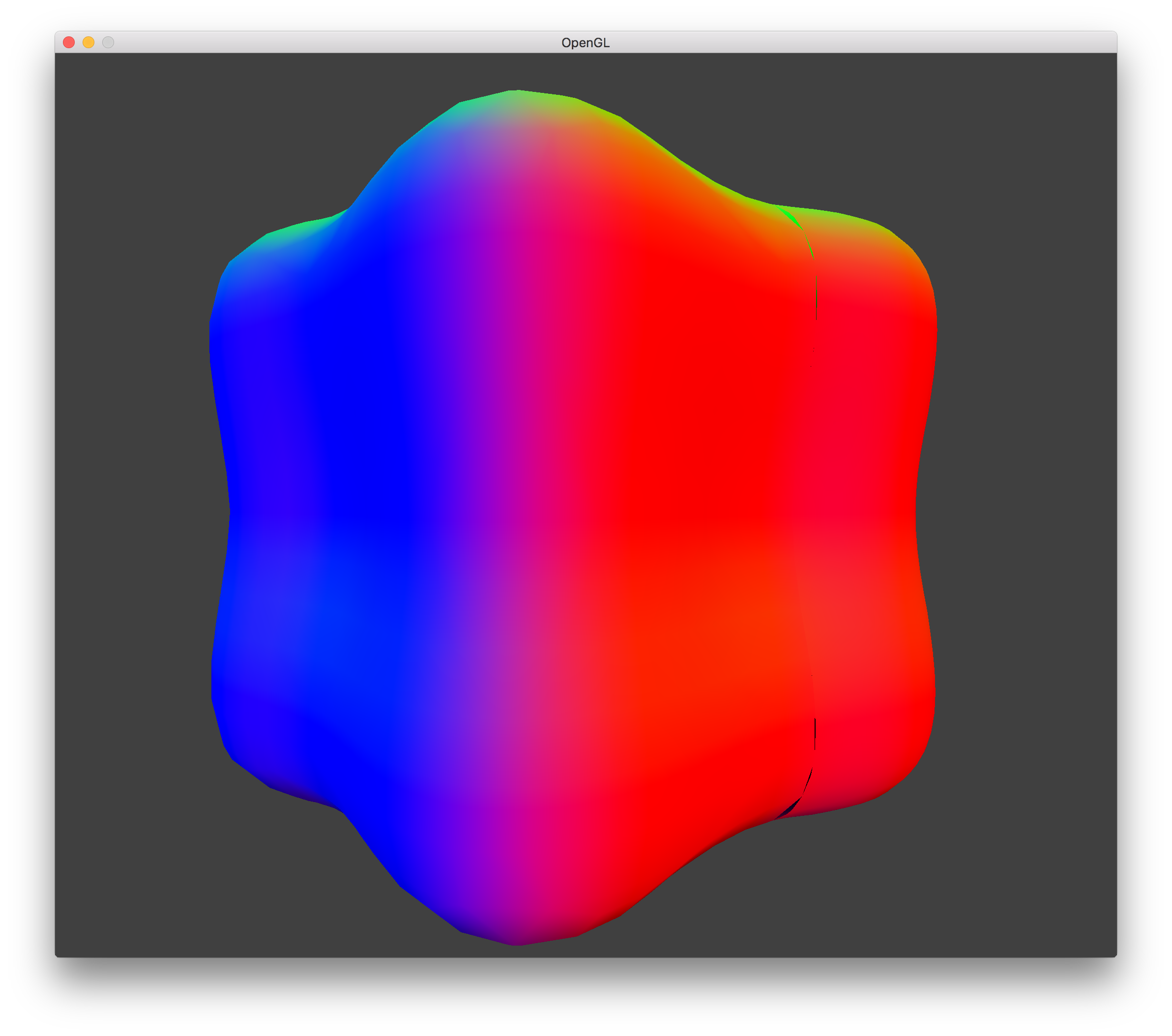
LOD 0 Hole w/ Surface Shifting

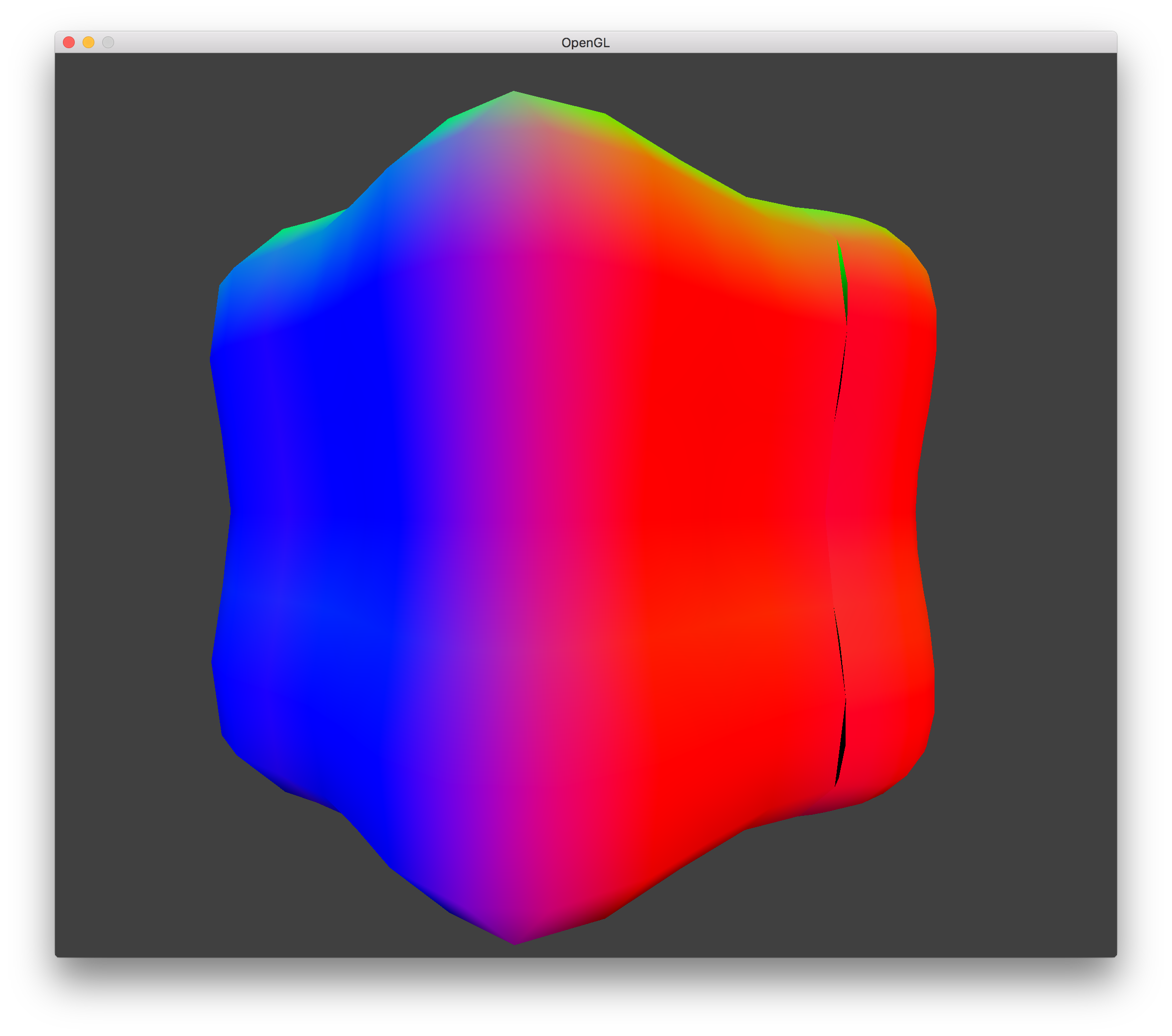
LOD 1 Hole w/ Surface Shifting

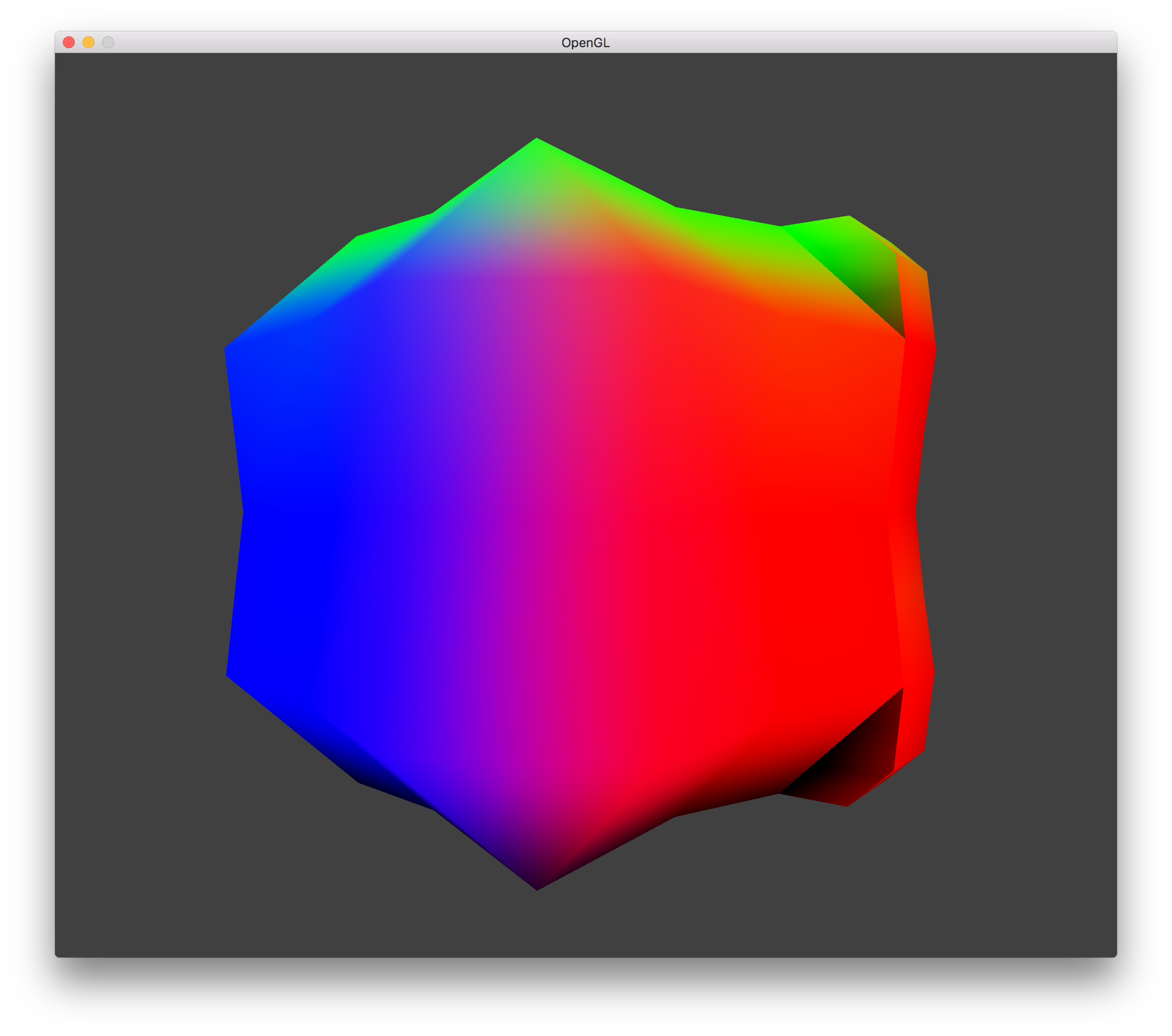
LOD 2 Hole w/ Surface Shifting

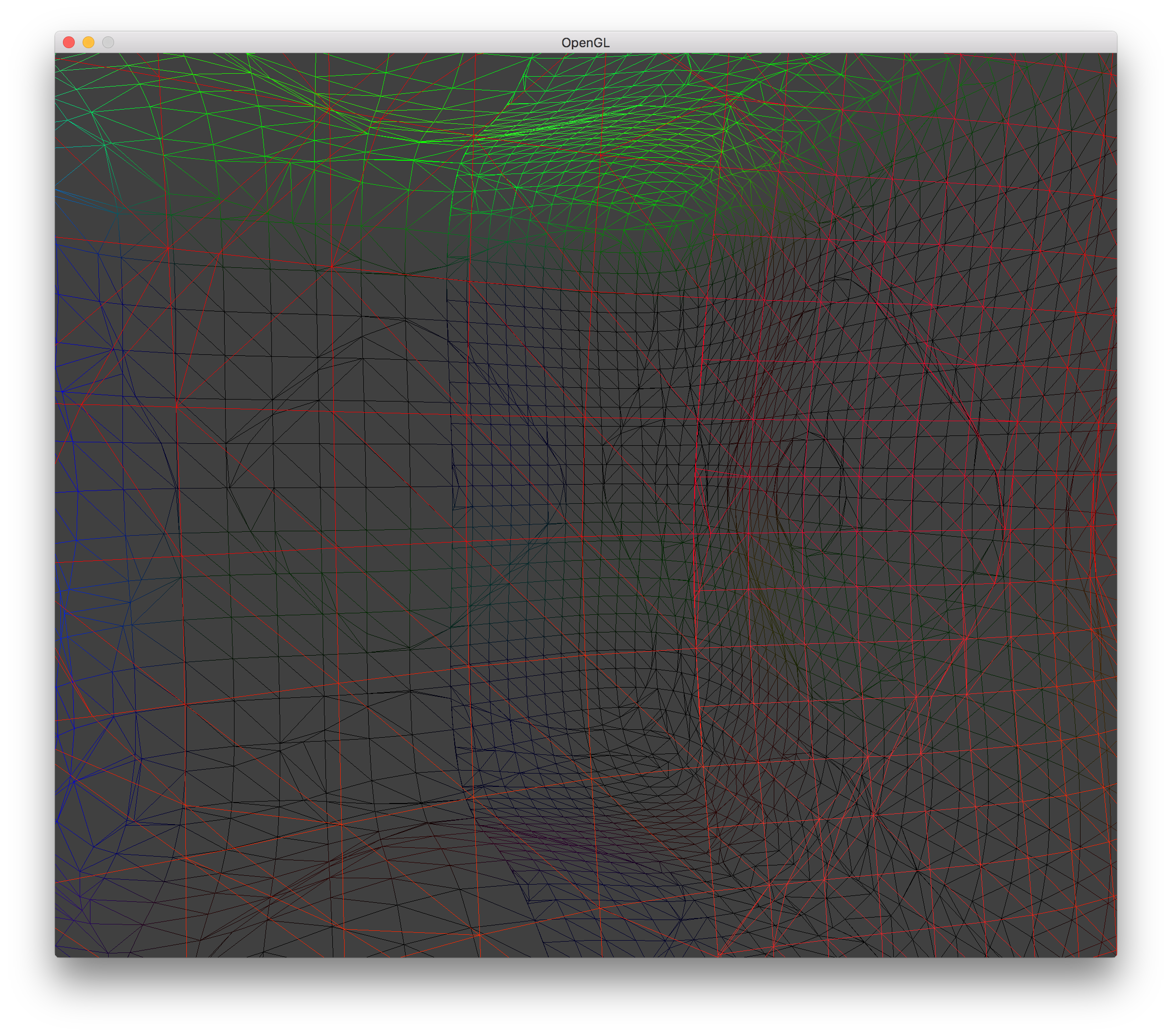
LOD 0 Hole w/ Surface Shifting Wireframe

LOD 1 Hole w/ Surface Shifting Wireframe

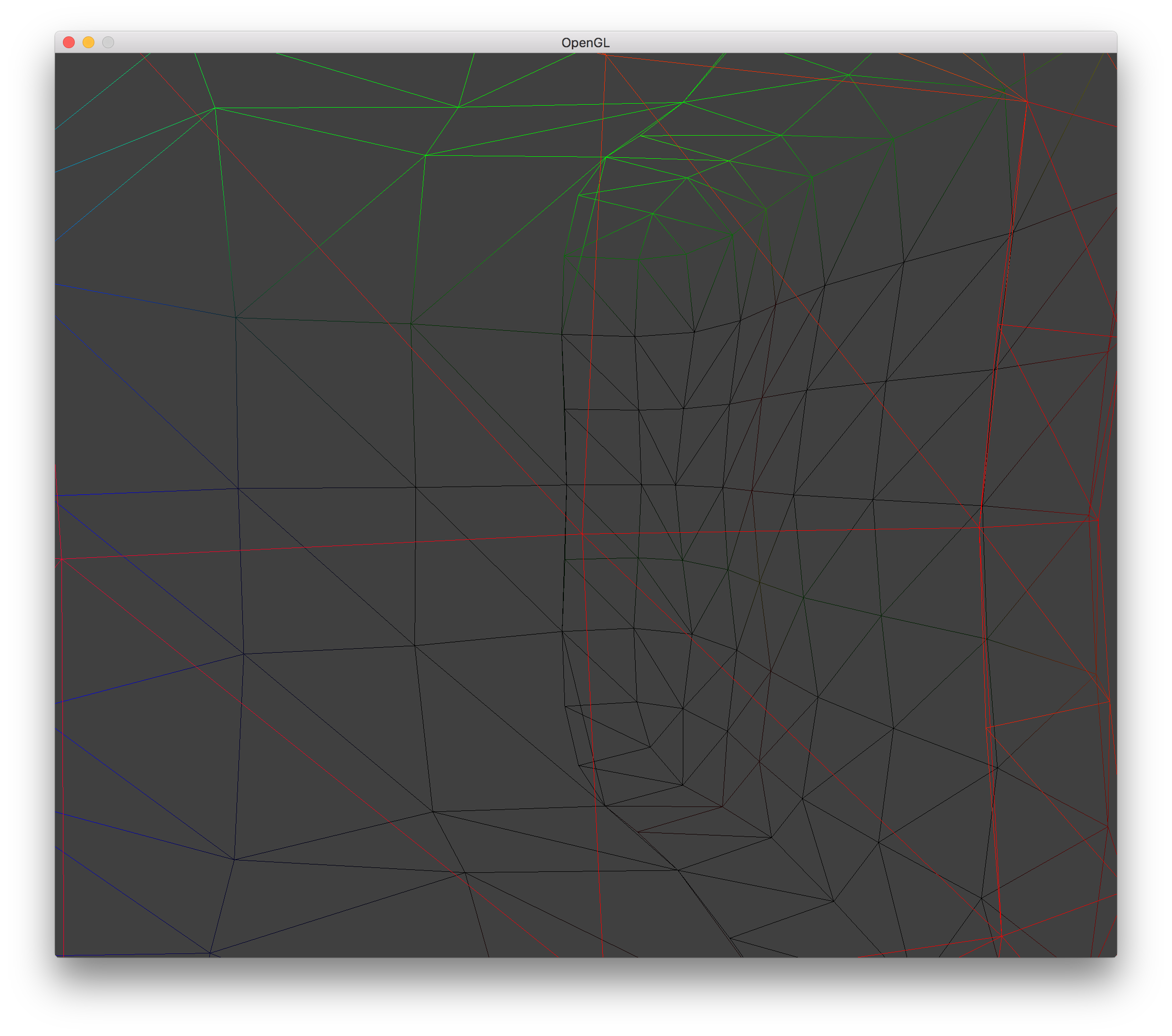
LOD 2 Hole w/ Surface Shifting Wireframe

Transvoxels (Ch 4)

The final step was to fill the holes generated from the LOD by using transition cells (transvoxels). This replaced any voxel along a lower resolution LOD boundary with 2+ voxels depending on how many sides were surrounded by higher resolution LOD (1 + #sides). The original voxel would still generate triangle vertices like normal, except it would only take up half of the space in whatever dimension the LOD boundary was. The other half of the space (the half closer to the higher resolution LOD) would be filled by a transvoxel.

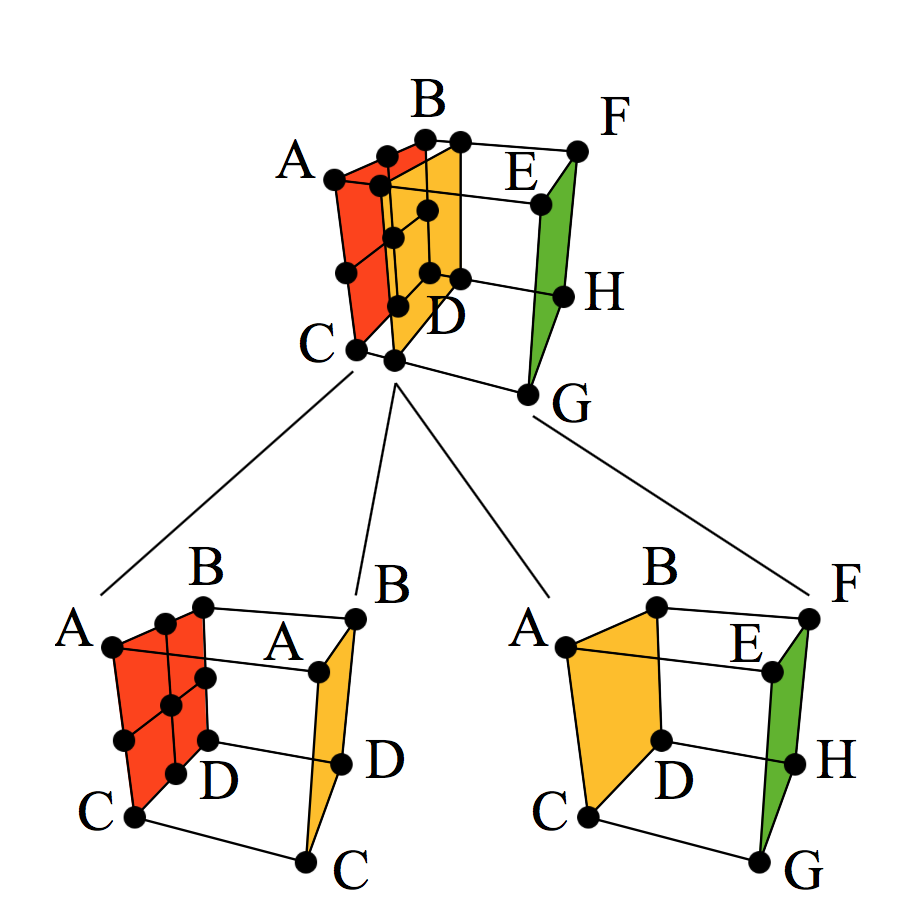
Transition Cell Diagram

A transvoxel consists of 13 points instead of the normal 8 (1 per corner). There are 9 points along the higher resolution LOD face, and 4 along the lower resolution LOD face. But the weird thing is that the 4 points along the lower resolution LOD face are actually the same isovalues as the 4 corners of the higher resolution LOD face. This allows much fewer possible configurations (512), which allowed Eric Lengyel to compute all possible vertex orientations for each configuration and put them into a table, just like for the Marching Cubes. The transvoxel tables are provided here.

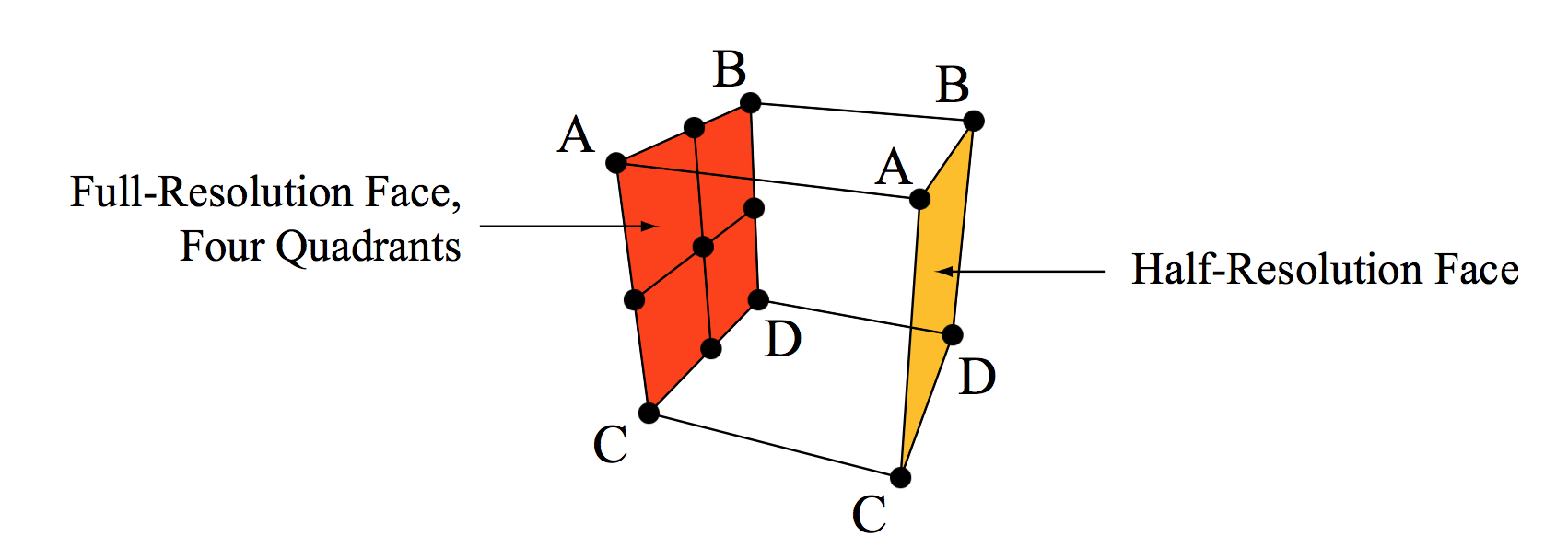
Transition Cell

Using the transvoxel tables, the process to generate triangle vertices is the same as for the normal Modified Marching Cubes. The amount of space the transvoxel takes up within the original voxel can be whatever you want, but Eric Lengyel recommended a value of 0.5 to ensure shading is normal and that no harsh changes in elevation occur in order to fill the holes.

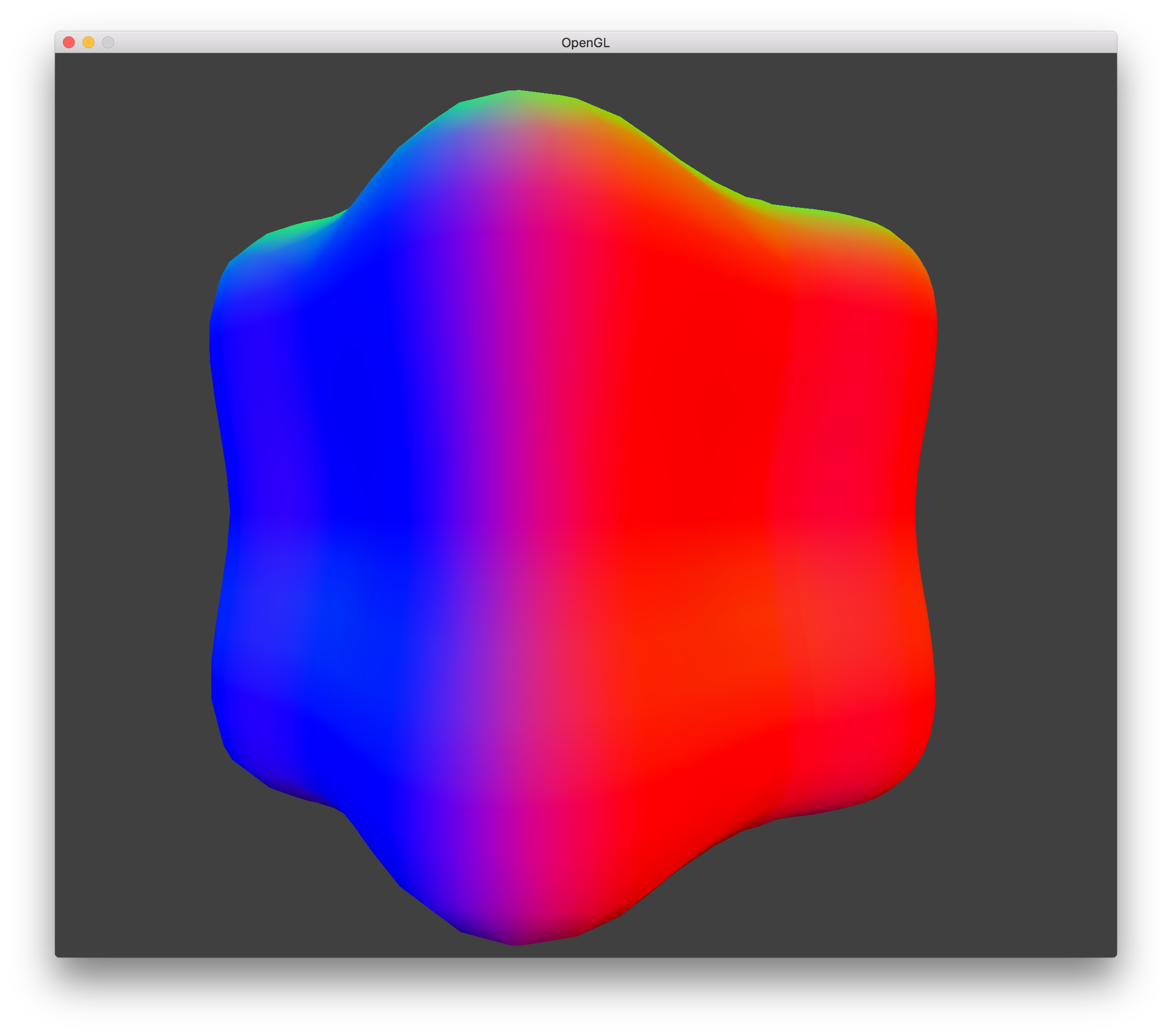
LOD 0 Transvoxels - No Holes

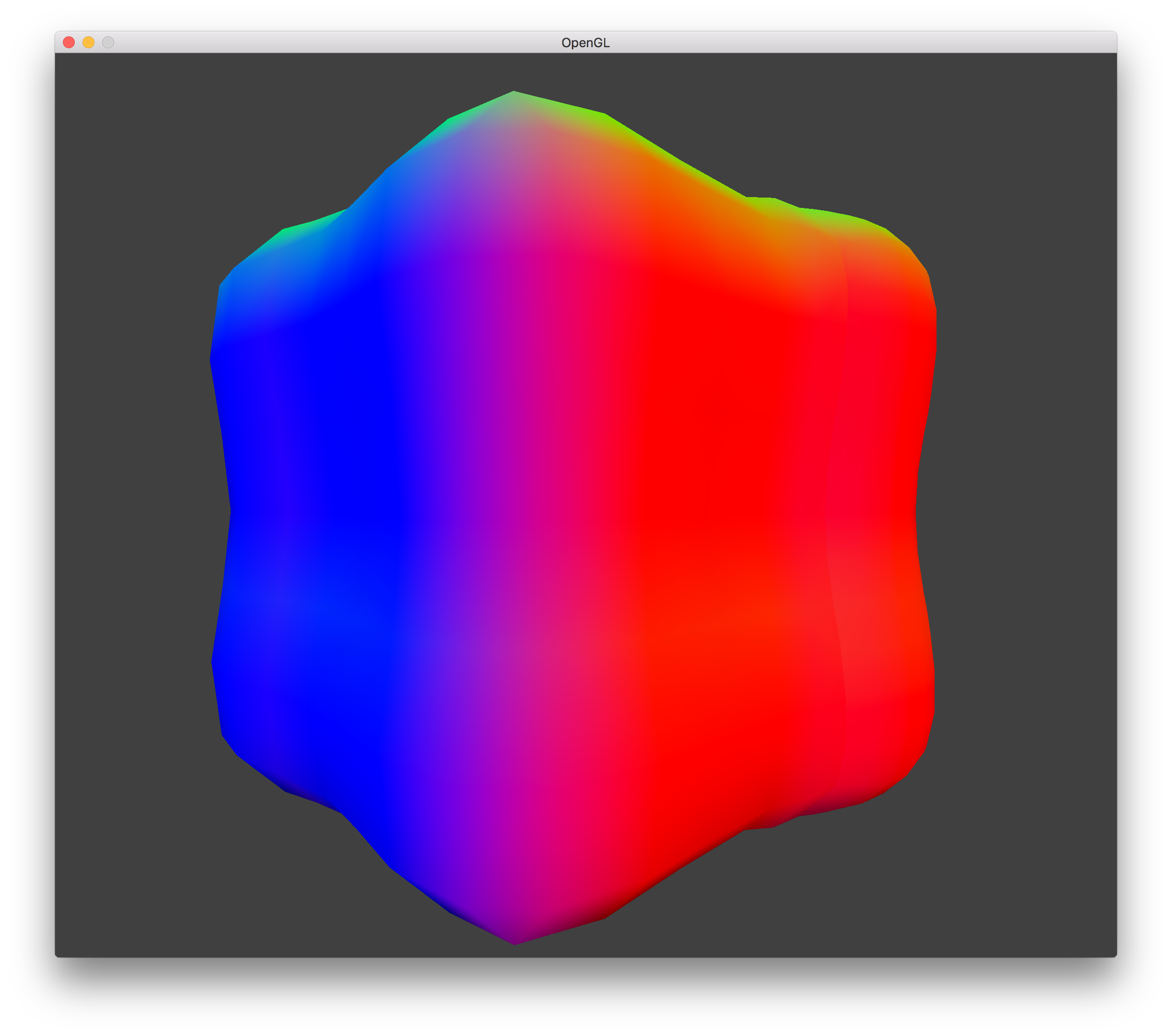
LOD 1 Transvoxels - No Holes

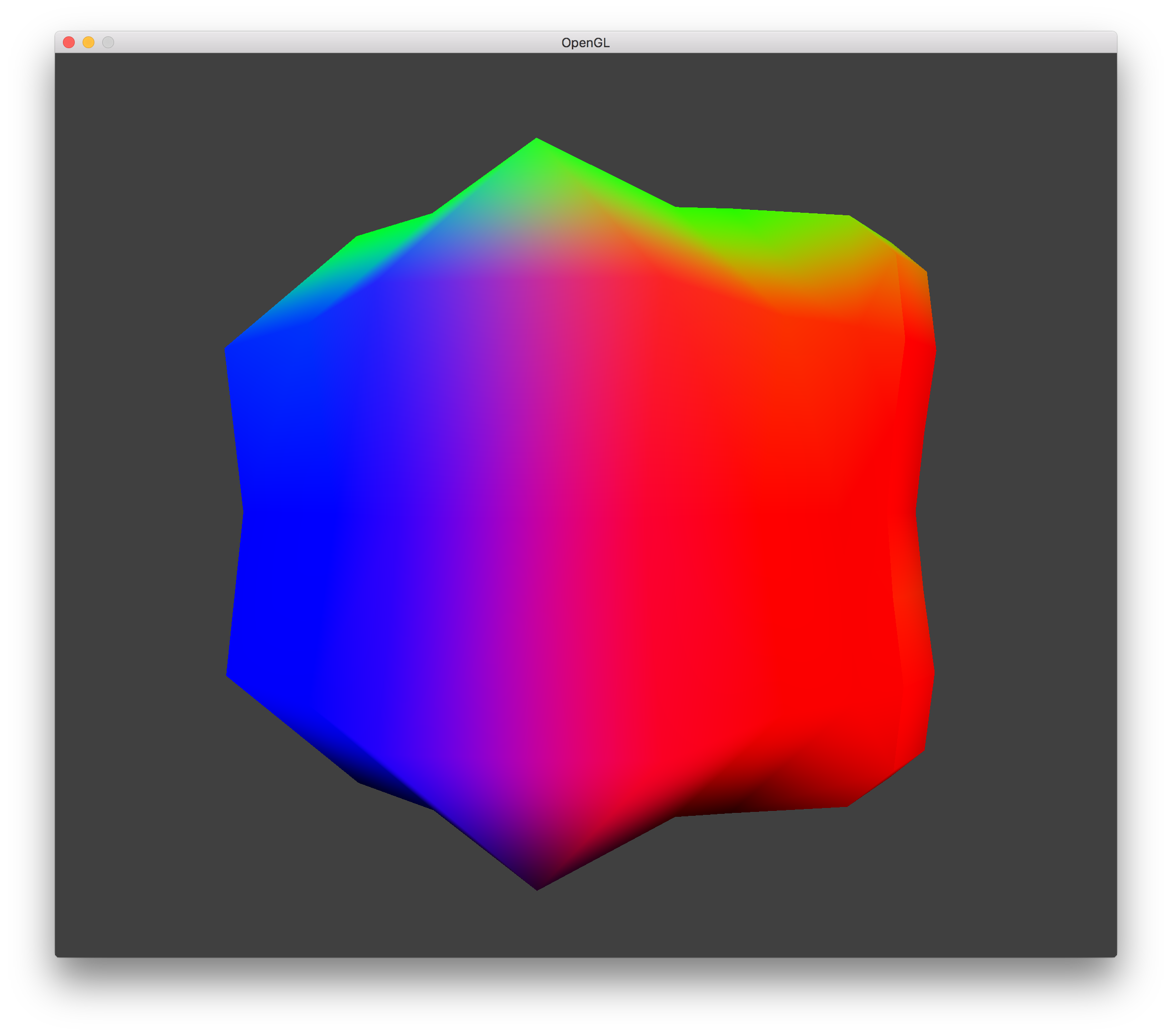
LOD 2 Transvoxels - No Holes

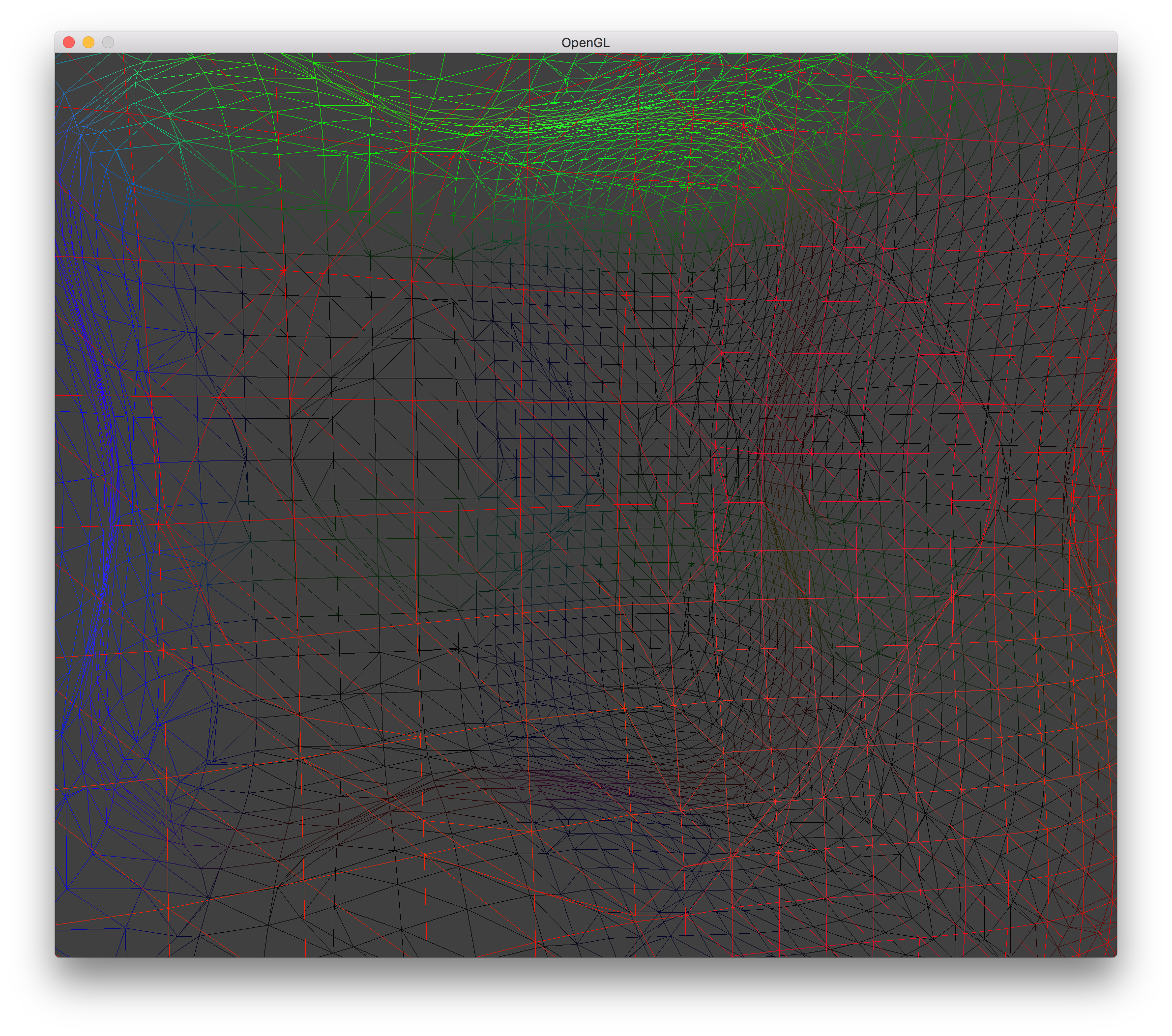
LOD 0 Transvoxels - No Holes Wireframe

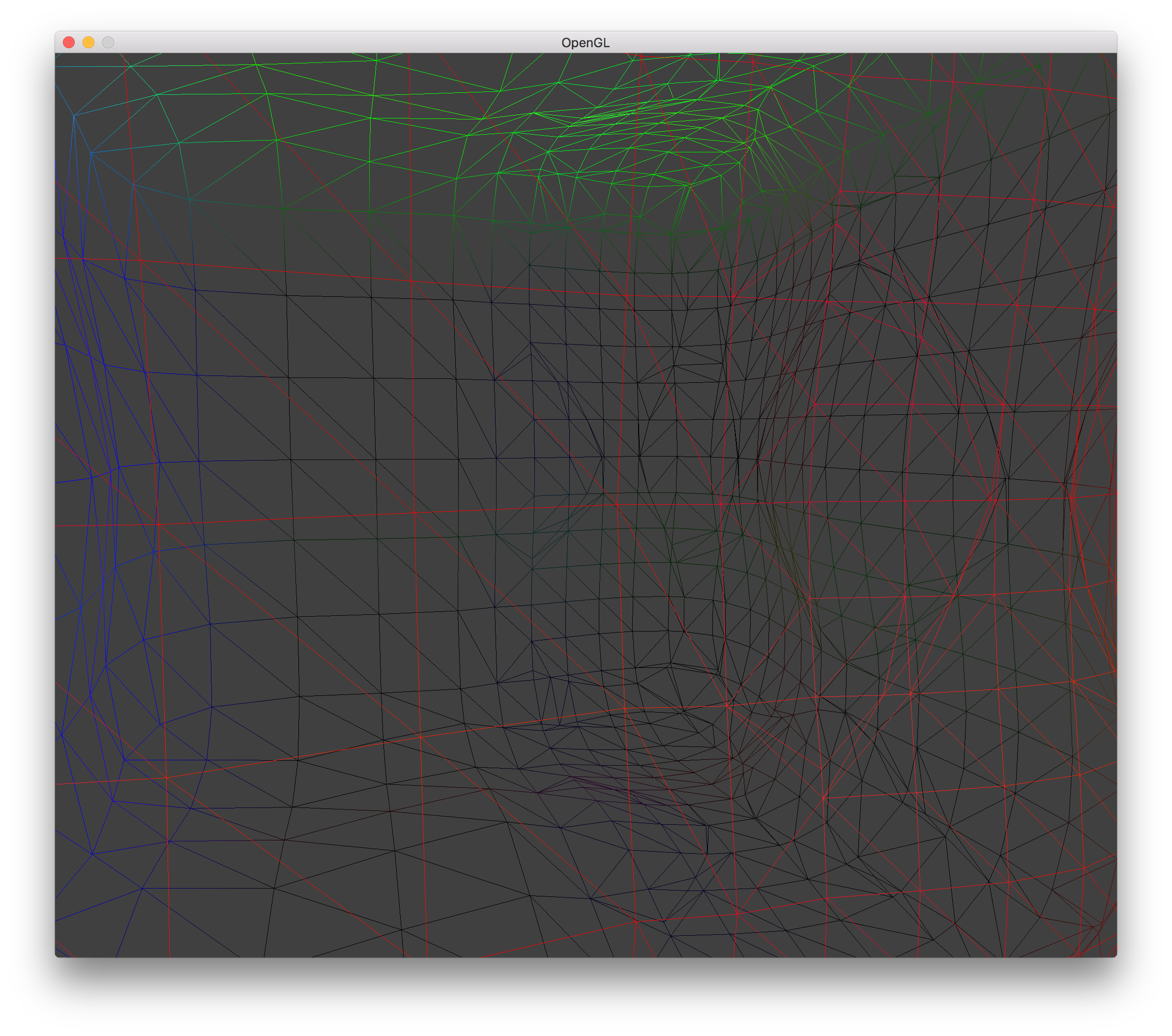
LOD 1 Transvoxels - No Holes Wireframe

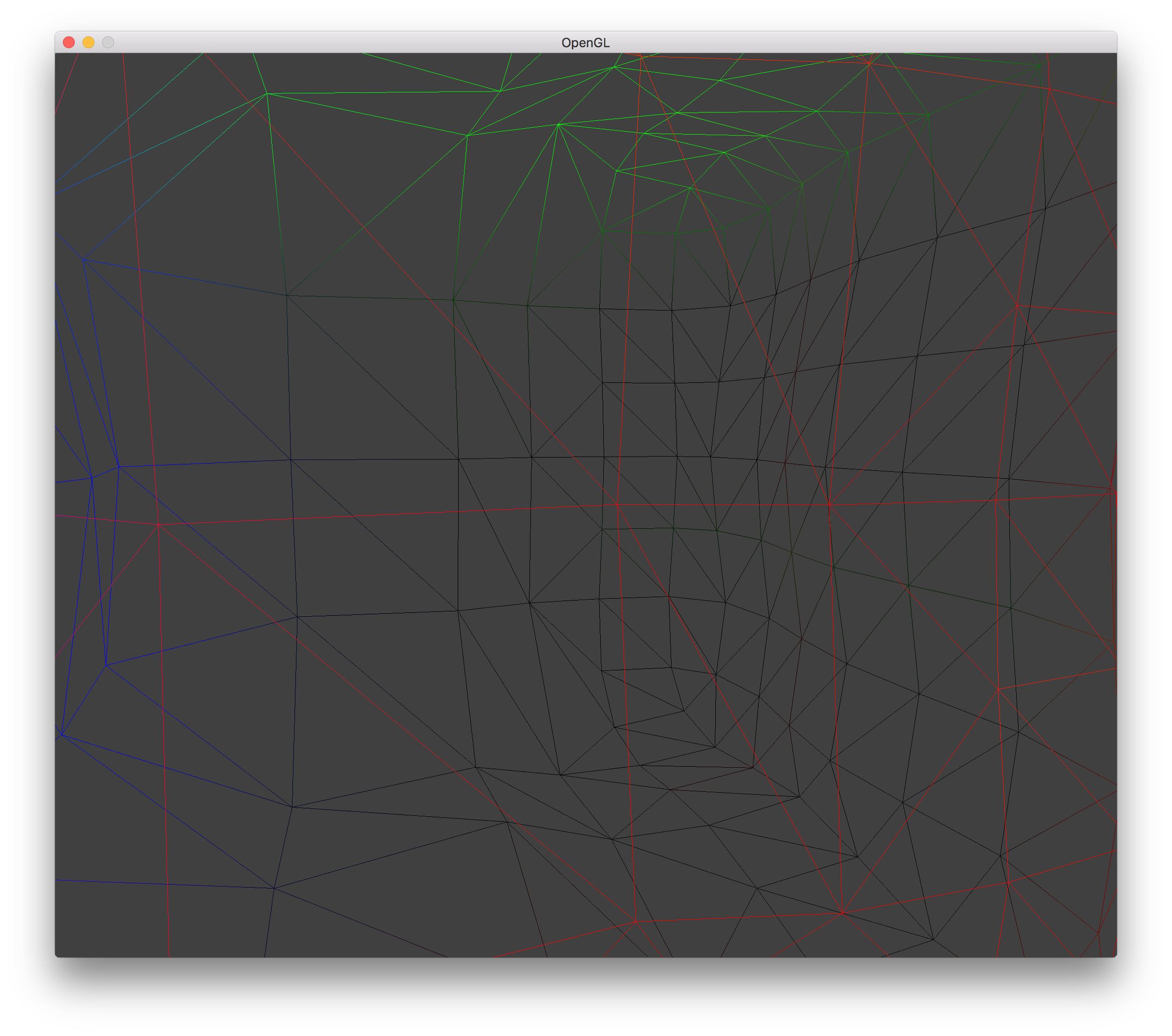
LOD 2 Transvoxels - No Holes Wireframe

Concavity Fixing

Even with the transvoxels correctly filling the holes, there can still be artifacts in the sense of concavities where the transvoxels are created. Instead of the geometry smoothly transitioning from one LOD to the next, a small concavity appears at the transition boundary. Eric Lengyel uses a linear transformation in order to fix this, but I was not able to get it working before the end of my project.

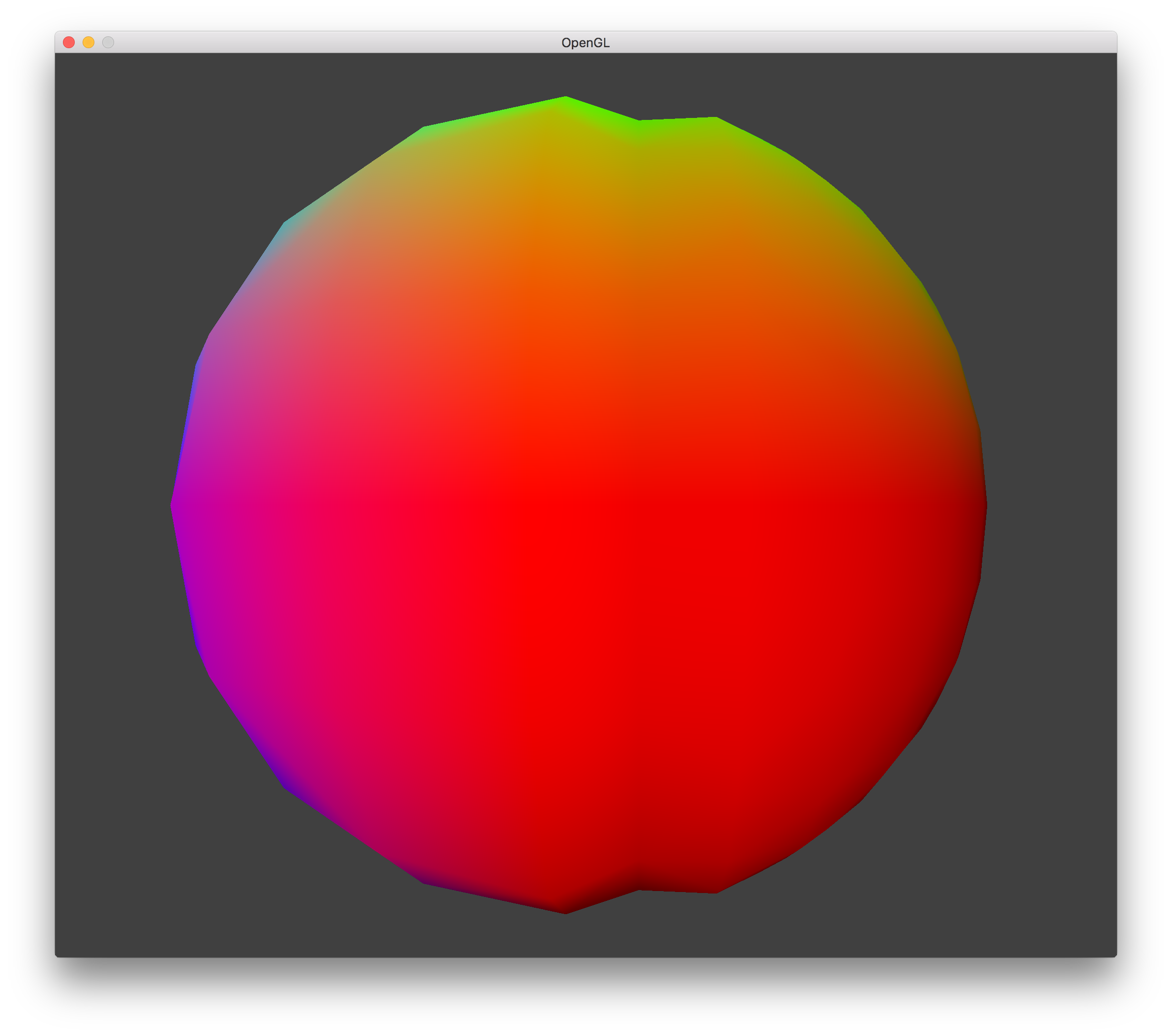
LOD 2 Concavity

LOD 2 Concavity Wireframe

Shading / Texturing (Ch 5)

Unfortunately, I didn't get this far... But it essentially used triplanar texturing and normal mapping to create pretty cool shading / texturing.

Triplanar Mapping

Triplanar + Normal Mapping

Terrain Editing

The Transvoxel Algorithm does not describe how to edit the terrain in detail, so I decided to implement my own method editing tool. The simplest tool I could think of was to cast a ray in the direction the camera is facing and to create a hole or create a column in that direction for each voxel that intersected the ray. When using a voxel volume of 64x64x64, it took a couple seconds to calculate this intersection for every voxel, so I sped it up by using a naive Octree space partition to detect voxel intersections with the ray. This sped it up by a factor of 100, which was adequate for real-time modifications.

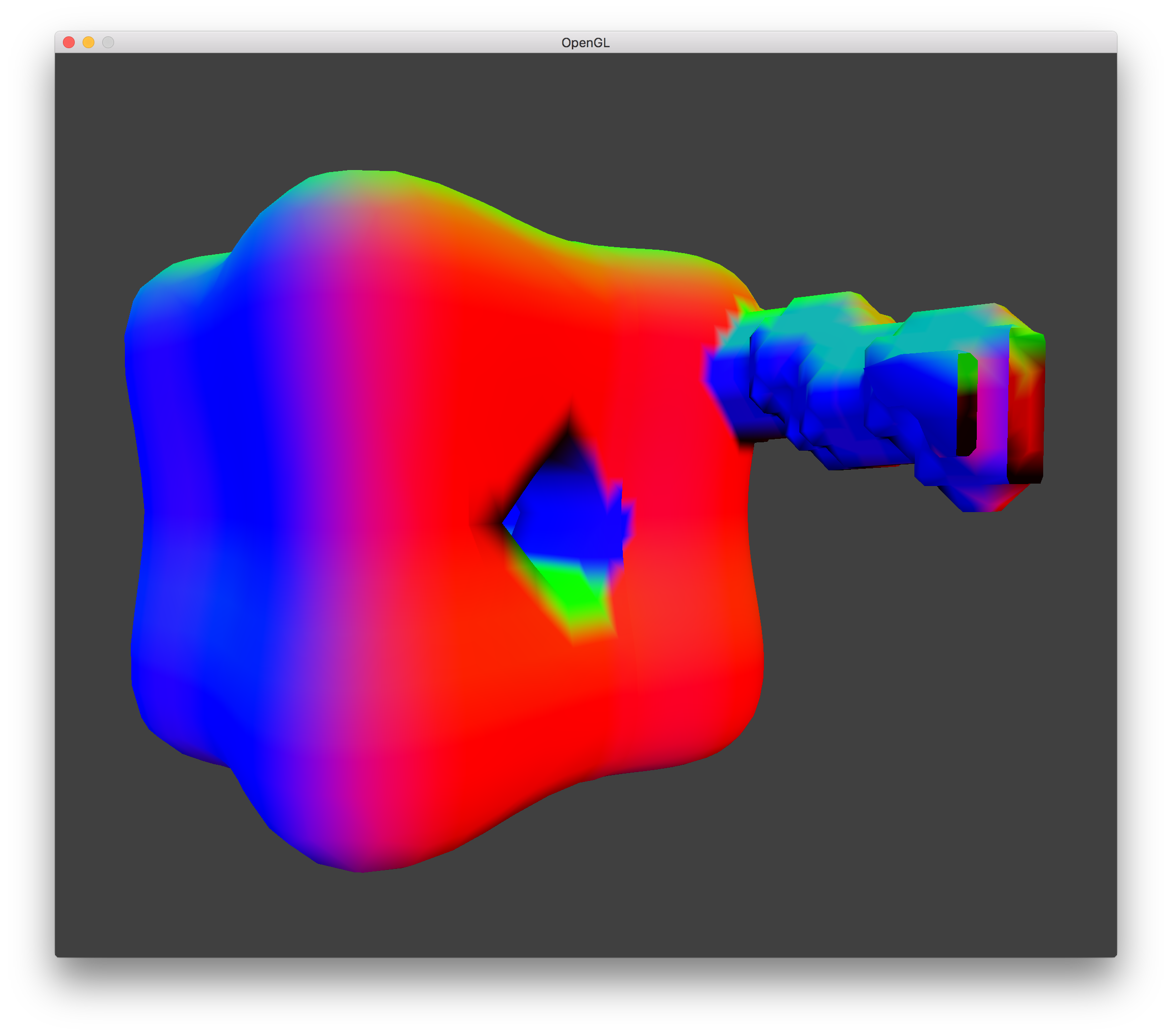
Editing a Cube

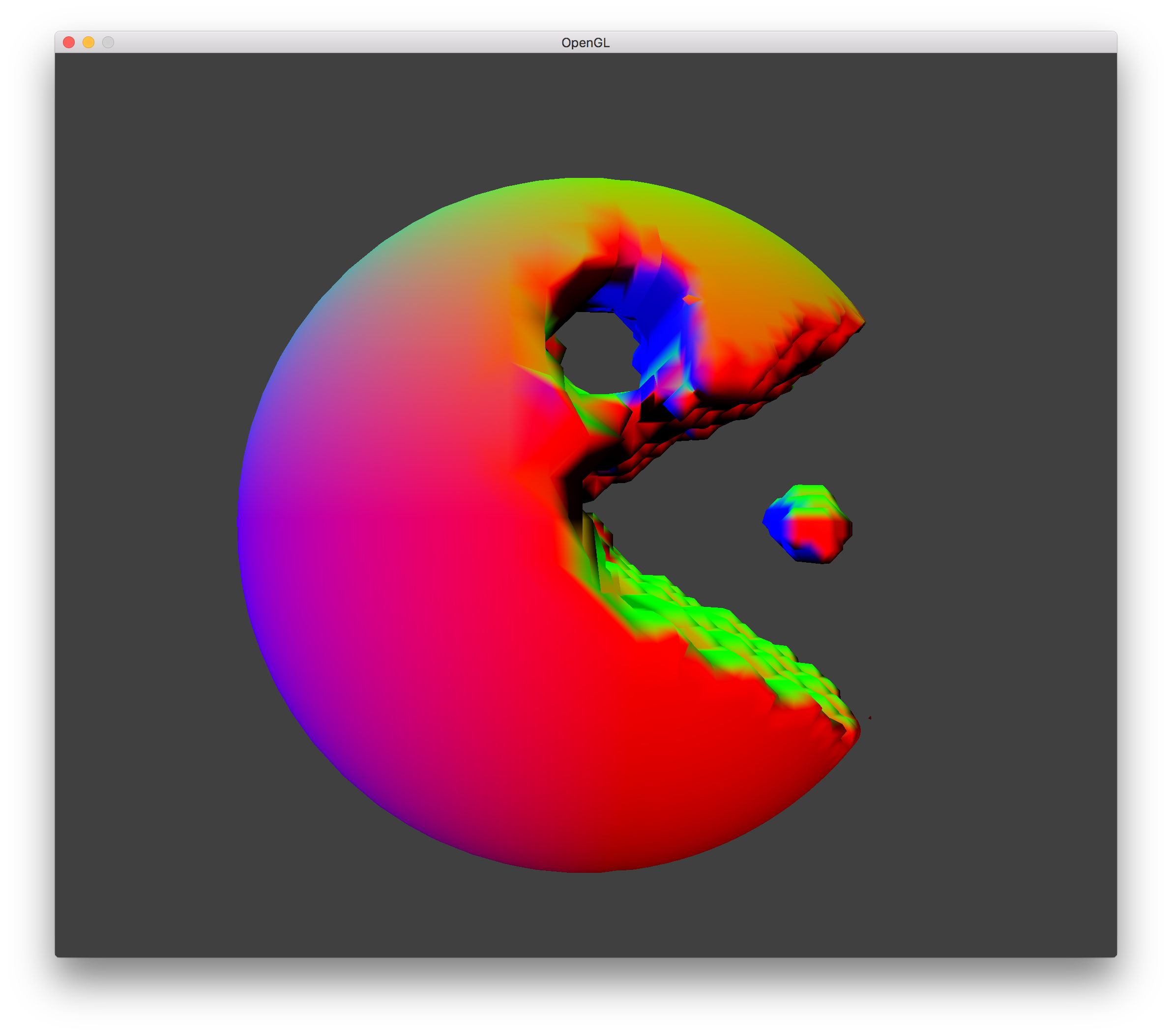
Editing a Sphere

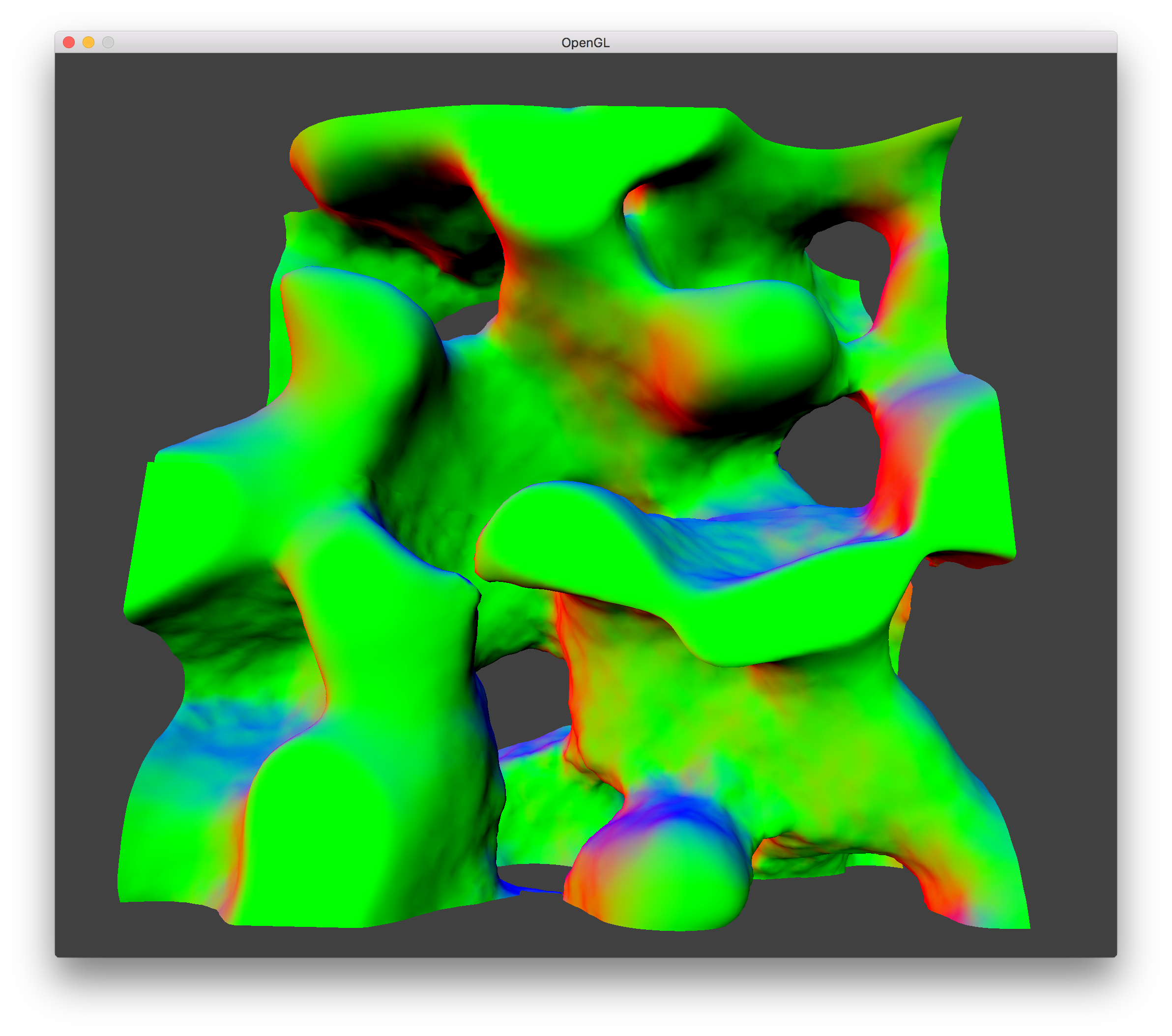
Terrain

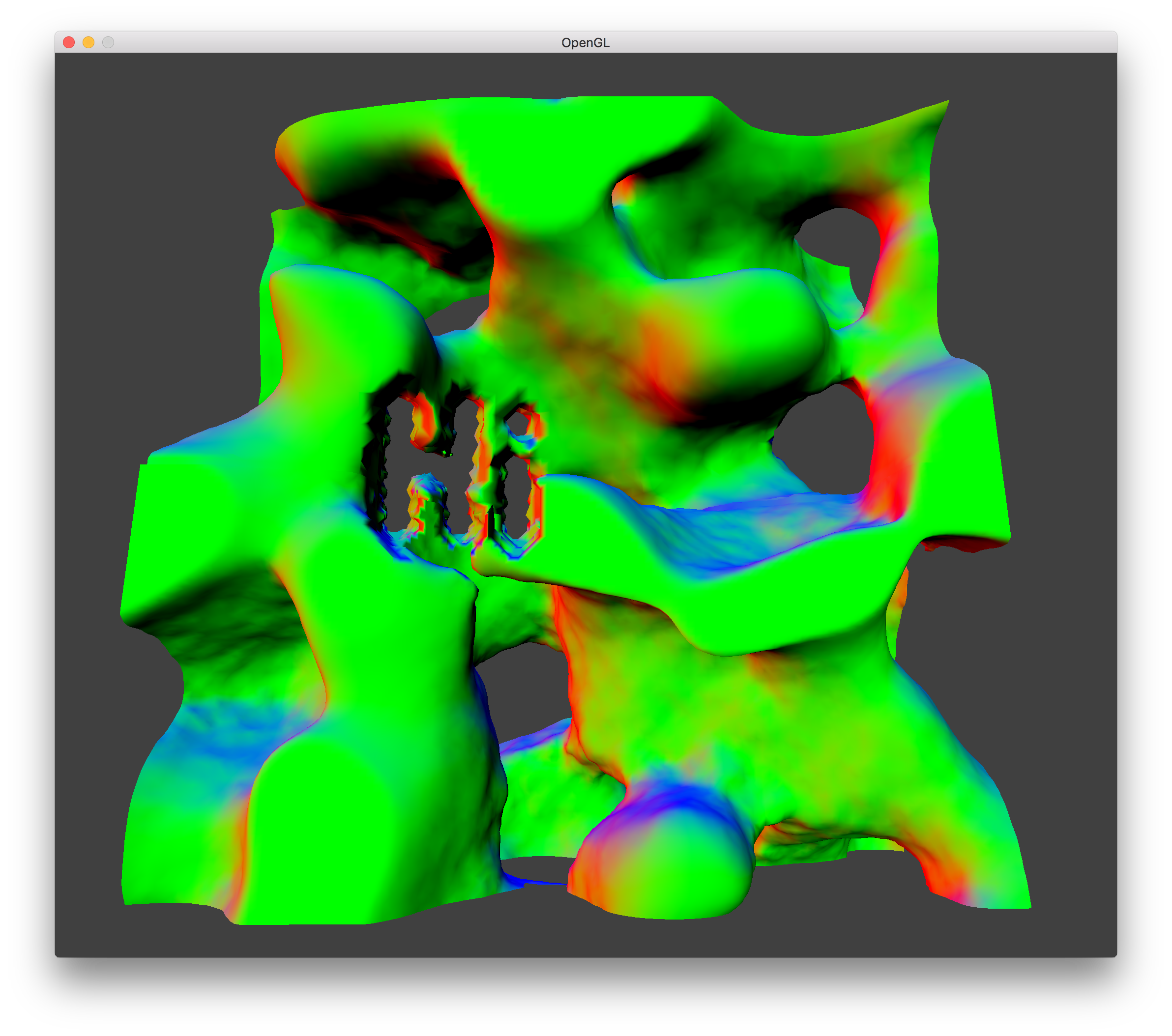
Editing Terrain

Conclusion

The transvoxel algorithm was pretty fun to implement, and has many applications in video games. I would have liked to implement the optimizations discussed in the paper as well, but I am pretty satisfied with the results I achieved. I used a 64x64x64 voxel volume for my implementation, but would have liked to try much larger volumes with LOD enabled, since LOD allows for vast landscapes to be rendered with much less computational overhead.